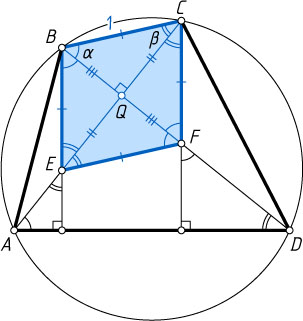
72. Четырёхугольник ABCD
, диагонали которого взаимно перпендикулярны, вписан в окружность. Перпендикуляры, опущенные на сторону AD
из вершин B
и C
, пересекают диагонали AC
и BD
в точках E
и F
соответственно. Найдите EF
, если BC=1
.
Ответ. 1.
Указание. Докажите, что BCFE
— параллелограмм.
Решение. Первый способ. Обозначим \angle CBD=\alpha
, \angle ACB=\beta
(\alpha+\beta=90^{\circ}
). Тогда
\angle CAD=\alpha,~\angle BEC=90^{\circ}-\alpha=\beta,~\angle DBE=\alpha.
Следовательно, BE=BC
.
Аналогично докажем, что \angle ACF=\beta
. Поэтому CF=BC
. Значит, BE=CF
, а так как BE\parallel CF
(перпендикуляры к одной и той же прямой AD
), то BCFE
— параллелограмм (даже ромб). Следовательно, EF=BC=1
.
Второй способ. Пусть Q
— точка пересечения диагоналей. Заметим, что E
— точка пересечения высот треугольника ABD
. По известному свойству ортоцентра треугольника EQ=QC
. Аналогично FQ=QB
. Поскольку диагонали четырёхугольника BCFE
перпендикулярны и делятся точкой пересечения Q
пополам, то BCFE
— ромб. Следовательно, EF=BC=1
.
Примечание. Верно более общее утверждение: если ABCD
— вписанный четырёхугольник, а H_{1}
и H_{2}
— точки пересечения высот треугольников ABD
и ACD
соответственно, то BCH_{1}H_{2}
— параллелограмм.
Источник: Вступительный экзамен на механико-математический факультет МГУ. — 1969, № 2, вариант 3
Источник: Прасолов В. В. Задачи по планиметрии. — 6-е изд. — М.: МЦНМО, 2007. — № 2.76, с. 38
