73. Около треугольника ABC
описана окружность. Медиана AD
продолжена до пересечения с этой окружностью в точке E
. Известно, что AB+AD=DE
, \angle BAD=60^{\circ}
, AE=6
. Найдите площадь треугольника ABC
.
Ответ. \frac{9\sqrt{3}}{4}
.
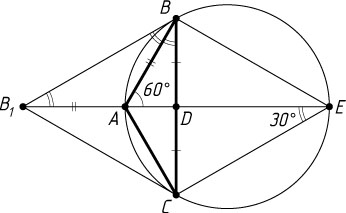
Указание. На продолжении отрезка EA
за точку A
отложите отрезок AB_{1}
, равный AB
. Четырёхугольник B_{1}BEC
— параллелограмм.
Решение. На продолжении отрезка EA
за точку A
отложим отрезок AB_{1}
, равный AB
. Тогда
B_{1}D=B_{1}A+AD=BA+AD=DE.
Следовательно, четырёхугольник B_{1}BEC
— параллелограмм. Тогда
\angle ABC=\angle B_{1}EC=\angle BB_{1}A=30^{\circ},~\angle ADB=90^{\circ},
поэтому AE
— диаметр окружности,
\angle ABE=90^{\circ},~AC=AB=\frac{1}{2}AE=3.
Следовательно,
S_{\triangle ABC}=\frac{1}{2}AB\cdot AC\sin\angle BAC=\frac{1}{2}\cdot3\cdot3\sin120^{\circ}=\frac{9\sqrt{3}}{4}.
Источник: Вступительный экзамен на механико-математический факультет МГУ. — 1974, вариант 1, № 3
Источник: Александров Б. И., Лурье М. В. Пособие по математике для поступающих в МГУ. — М.: Изд-во МГУ, 1977. — с. 277
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — № 11.37, с. 89
