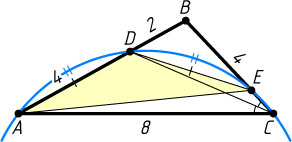
74. В треугольнике ABC
известны стороны: AB=6
, BC=4
, AC=8
. Биссектриса угла C
пересекает сторону AB
в точке D
. Через точки A
, D
и C
проведена окружность, пересекающая сторону BC
в точке E
. Найдите площадь треугольника ADE
.
Ответ. \frac{3\sqrt{15}}{2}
.
Указание. Треугольник ADE
— равнобедренный, \sin\angle ADE=\sin\angle ACB
.
Решение. По свойству биссектрисы треугольника \frac{AD}{DB}=\frac{AC}{BC}=\frac{2}{1}
. Тогда DE=AD=4
.
Поскольку четырёхугольник ADEC
— вписанный, то \sin\angle ADE=\sin\angle ACB
. По теореме косинусов
\cos\angle ACB=\frac{AC^{2}+BC^{2}-AB^{2}}{2AC\cdot BC}=\frac{11}{16}.
Тогда \sin\angle ACB=\frac{3\sqrt{15}}{16}
. Следовательно,
S_{\triangle ADE}=\frac{1}{2}AD\cdot DE\sin\angle ADE=\frac{1}{2}AD\cdot DE\sin\angle ACB=\frac{3\sqrt{15}}{2}.
Источник: Вступительный экзамен на геологический факультет МГУ. — 1975, вариант 1, № 4
Источник: Александров Б. И., Лурье М. В. Пособие по математике для поступающих в МГУ. — М.: Изд-во МГУ, 1977. — с. 147
