79. Из точки P
, расположенной внутри острого угла BAC
, опущены перпендикуляры PC_{1}
и PB_{1}
на прямые AB
и AC
. Докажите, что \angle C_{1}AP=\angle C_{1}B_{1}P
.
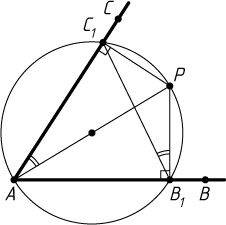
Указание. Точки C_{1}
, A
, B_{1}
и P
лежат на одной окружности.
Решение. Поскольку отрезок AP
виден из точек B_{1}
и C_{1}
под прямым углом, то точки C_{1}
и B_{1}
лежат на окружности с диаметром AP
. Следовательно,
\angle C_{1}AP=\angle C_{1}B_{1}P
как вписанные углы, опирающиеся на одну и ту же дугу.
Источник: Прасолов В. В. Задачи по планиметрии. — 6-е изд. — М.: МЦНМО, 2007. — № 2, с. 31
