81. На сторонах AC
и BC
треугольника ABC
во внешнюю сторону построены квадраты ACA_{1}A_{2}
и BCB_{1}B_{2}
. Докажите, что прямые A_{1}B
, A_{2}B_{2}
и AB_{1}
пересекаются в одной точке.
Указание. Опишите окружности около квадратов и рассмотрите точку пересечения этих окружностей, отличную от C
.
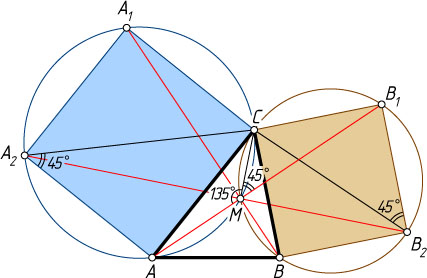
Решение. Опишем окружности около этих квадратов. Пусть M
— общая точка этих окружностей, отличная от C
. Тогда
\angle CMB_{1}=\angle CB_{2}B_{1}=45^{\circ},~\angle CMA=180^{\circ}-\angle CA_{2}A=135^{\circ}.
Следовательно, прямая AB_{1}
проходит через точку M
.
Аналогично для прямых A_{2}B_{2}
и AB_{1}
.
Источник: Прасолов В. В. Задачи по планиметрии. — Ч. 1. — М.: Наука, 1991. — № 2.92, с. 41
Источник: Прасолов В. В. Задачи по планиметрии. — 6-е изд. — М.: МЦНМО, 2007. — № 2.97, с. 41
