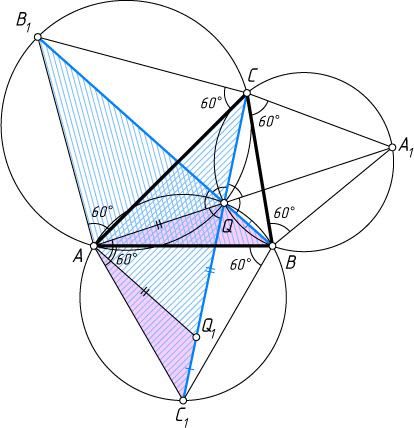
82. На сторонах произвольного треугольника ABC
во внешнюю сторону построены равносторонние треугольники ABC_{1}
, A_{1}BC
и AB_{1}C
. Докажите, что прямые AA_{1}
, BB_{1}
и CC_{1}
пересекаются в одной точке.
Решение. При повороте на угол 60^{\circ}
вокруг вершины A
, переводящем точку C_{1}
в B
, точка C
переходит в точку B_{1}
. Следовательно, прямая C_{1}C
переходит в прямую BB_{1}
. Поэтому угол между этими прямыми равен 60^{\circ}
.
Пусть Q
— точка пересечения прямых BB_{1}
и CC_{1}
. Отрезок C_{1}B
виден из точек A
и Q
под углом 60^{\circ}
. Поэтому точка Q
лежит на описанной окружности треугольника ABC_{1}
. Аналогично докажем, что точка Q
лежит на описанной окружности треугольника CAB_{1}
. Поскольку
\angle BQC+\angle BA_{1}C=120^{\circ}+60^{\circ}=180^{\circ},
точка Q
лежит и на описанной окружности треугольника BCA_{1}
. Тогда
\angle AQA_{1}=\angle AQB+\angle BQA_{1}=\angle AQB+\angle BCA_{1}=120^{\circ}+60^{\circ}=180^{\circ}.
Значит, прямая AA_{1}
проходит через точку Q
. Следовательно, все три прямые AA_{1}
, BB_{1}
и CC_{1}
пересекаются в точке Q
.