84. В треугольнике ABC
стороны AC
и BC
не равны. Докажите, что биссектриса угла C
делит пополам угол между медианой и высотой, проведёнными из вершины C
, тогда и только тогда, когда \angle C=90^{\circ}
.
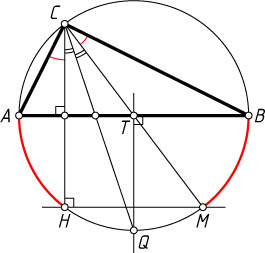
Указание. Пусть H
, Q
, M
— точки пересечения продолжений высоты, биссектрисы и медианы с описанной окружностью. Тогда HM\parallel AB
.
Решение. Пусть T
— середина AB
. Опишем окружность около треугольника ABC
. Продолжения высоты, биссектрисы и медианы пересекают эту окружность в точках H
, Q
и M
соответственно.
Необходимость. Поскольку дуги AH
и MB
равны, то HM\parallel AB
. Поэтому \angle CHM=90^{\circ}
и CM
— диаметр окружности. Поскольку точки Q
и T
равноудалены от концов отрезка AB
, то QT
— серединный перпендикуляр к стороне AB
, поэтому T
— центр окружности. Следовательно, AB
— также диаметр.
Достаточность. Пусть угол C
— прямой. Тогда CM
— диаметр, угол CHM
— прямой. Поэтому HM\parallel AB
. Отсюда следует, что
\cup AH=\cup MB,~\angle ACH=\angle MCB.
Поэтому \angle HCQ=\angle MCQ
.
Источник: Прасолов В. В. Задачи по планиметрии. — Ч. 1. — М.: Наука, 1991. — № 2.65 с. 38
Источник: Прасолов В. В. Задачи по планиметрии. — 6-е изд. — М.: МЦНМО, 2007. — № 2.68, с. 37
Источник: Куланин Е. Д., Федин С. Н. Геометрия треугольника в задачах: Экспериментальное учебное пособие для 8—10 кл. школ физико-математического направления. — М.: НИИ школ, 1990. — № 9, с. 30
Источник: Моденов П. С. Сборник задач по специальному курсу элементарной математики. — М.: Советская наука, 1957. — № 29, с. 184
