86. С помощью циркуля и линейки постройте треугольник по точкам пересечения с описанной окружностью его высоты, медианы и биссектрисы, проведённых из одной вершины.
Решение. Пусть известно, что H
, Q
и M
— точки пересечения с описанной окружностью треугольника ABC
соответственно высоты, биссектрисы и медианы, проведённых из вершины C
.
Предположим, что треугольник ABC
построен. Поскольку CQ
— биссектриса вписанного угла ACB
, то Q
— середина дуги AB
, не содержащей точки C
. Если XY
— произвольная хорда описанной окружности треугольника ABC
, параллельная AB
, то Q
— середина дуги XY
, не содержащей точки C
.
Точка Q
и середина T
хорды AB
лежат не серединном перпендикуляре к AB
. Поэтому,
QT\parallel CH,~QT\perp XY,~CH\perp XY.
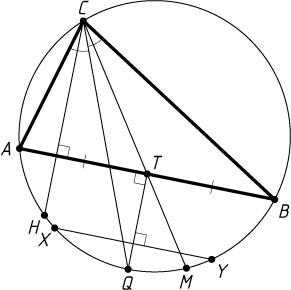
Отсюда вытекает следующее построение. Описываем окружность около данного треугольника HQM
. Строим на этой окружности две точки X
и Y
, равноудалённые от точки Q
. Через точку H
проводим прямую, перпендикулярную XY
. Эта прямая вторично пересекает окружность в вершине C
искомого треугольника. Через точку Q
проводим прямую, также перпендикулярную XY
. Пусть эта прямая пересекается с прямой CM
в точке T
. Через точку T
проводим прямую, перпендикулярную CH
. Эта прямая пересекает окружность в искомых вершинах A
и B
.
Докажем, что построен искомый треугольник ABC
. Действительно, CH\perp AB
по построению. Точка Q
— середина дуги AB
, не содержащей точки C
(так как дуги, заключённые между параллельными хордами XY
и AB
равны), а Q
— середина дуги XY
по построению. Следовательно, CQ
— биссектриса угла BAC
. Из построения также следует, что QT\perp AB
и QA=QB
. Значит, T
— середина AB
. Поэтому M
— точка пересечения продолжения медианы CT
с описанной окружностью треугольника ABC
.
Источник: Московская математическая олимпиада. — 1935, I, 2-й тур
Источник: Вступительный экзамен в МФТИ. — 1958, билет 16, № 2
Источник: Сборник методических материалов письменных испытаний по математике и физике абитуриентов Московского Физтеха (1947—2006 гг.). Математика / Сост. Д. А. Александров, И. Г. Почернин, И. Г. Проценко, И. Е. Сидорова, В. Б. Трушин, И. Г. Шомполов. Под ред. И. Г. Шомполова. — М.: МФТИ, 2007. — № 58-16-2, с. 66
Источник: Гальперин Г. А., Толпыго А. К. Московские математические олимпиады. — М.: Просвещение, 1988. — № 4, с. 20
Источник: Шклярский Д. О., Ченцов Н. Н., Яглом И. М. Избранные задачи и теоремы элементарной математики. — Ч. 2: Геометрия (планиметрия). — М.: ГТТИ, 1952. — № 66, с. 24
Источник: Куланин Е. Д., Федин С. Н. Геометрия треугольника в задачах: Экспериментальное учебное пособие для 8—10 кл. школ физико-математического направления. — М.: НИИ школ, 1990. — № 17а, с. 57
Источник: Прасолов В. В. Задачи по планиметрии. — 6-е изд. — М.: МЦНМО, 2007. — № 8.32, с. 199
