87. Докажите, что угол между касательной и хордой, проведённой через точку касания, равен половине угловой величины дуги, заключённой между ними.
Указание. Касательная перпендикулярна радиусу, проведённому в точку касания.
Решение. Пусть AB
— хорда, AM
— касательная, O
— центр окружности. Обозначим через \alpha
градусную меру меньшей дуги AB
.
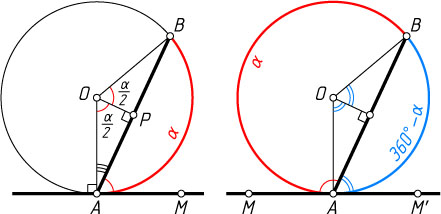
Первый способ. Пусть \angle MAB\lt90^{\circ}
. Из центра окружности опустим перпендикуляр OP
на AB
. Тогда каждый из углов MAB
и AOP
дополняет угол OAB
до 90^{\circ}
. Следовательно,
\angle MAB=\angle AOP=\frac{1}{2}\angle AOB=\frac{1}{2}\alpha.
Пусть \angle MAB\gt90^{\circ}
. На луче, дополнительном к лучу AM
, возьмём точку M'
. Тогда \angle M'AB\lt90^{\circ}
. По доказанному \angle M'AB=\frac{1}{2}\angle AOB
, поэтому
\angle MAB=180^{\circ}-\angle M'AB=180^{\circ}-\frac{1}{2}\alpha=\frac{1}{2}(360^{\circ}-\alpha).
Осталось заметить, что 360^{\circ}-\alpha
— градусная мера дуги, заключённой внутри угла MAB
.
Если \angle MAB=90^{\circ}
, то утверждение очевидно.
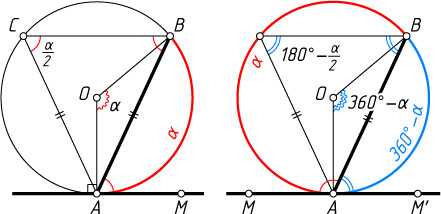
Второй способ. Пусть \angle MAB\lt90^{\circ}
. Через точку B
проведём хорду BC
, параллельную AM
. Тогда
\angle MAB=\angle ABC=\angle ACB=\frac{1}{2}\alpha.
Пусть \angle MAB\gt90^{\circ}
. На луче, дополнительном к лучу AM
, возьмём точку M'
. Тогда \angle M'AB\lt90^{\circ}
. По доказанному \angle M'AB=\frac{1}{2}\angle AOB
, поэтому
\angle MAB=180^{\circ}-\angle M'AB=180^{\circ}-\frac{1}{2}\alpha=\frac{1}{2}(360^{\circ}-\alpha).
Осталось заметить, что 360^{\circ}-\alpha
— градусная мера дуги, заключённой внутри угла MAB
.
Если \angle MAB=90^{\circ}
, то утверждение очевидно.
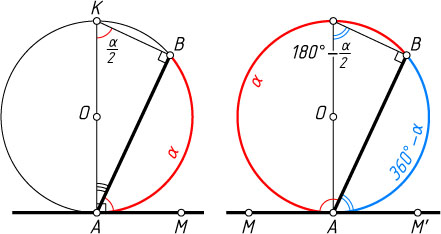
Третий способ. Пусть \angle MAB\lt90^{\circ}
. Продолжим AO
до пересечения с окружностью в точке K
и соединим точки K
и B
. Тогда \angle ABK=90^{\circ}
. Поэтому
\angle MAB=\angle KAM-\angle KAB=90^{\circ}-\angle KAB=\angle AKB=\frac{1}{2}\alpha.
Пусть \angle MAB\gt90^{\circ}
. На луче, дополнительном к лучу AM
, возьмём точку M'
. Тогда \angle M'AB\lt90^{\circ}
. По доказанному \angle M'AB=\frac{1}{2}\angle AOB
, поэтому
\angle MAB=180^{\circ}-\angle M'AB=180^{\circ}-\frac{1}{2}\alpha=\frac{1}{2}(360^{\circ}-\alpha).
Осталось заметить, что 360^{\circ}-\alpha
— градусная мера дуги, заключённой внутри угла MAB
.
Если \angle MAB=90^{\circ}
, то утверждение очевидно.
Источник: Адамар Ж. Элементарная геометрия. — Ч. 1: Планиметрия. — М.: Учпедгиз, 1948. — с. 72
Источник: Атанасян Л. С. и др. Геометрия 7—9: Учебник для 7—9 кл. средней школы. — М.: Просвещение, 1990. — № 664, с. 167
Источник: Шарыгин И. Ф. Геометрия: 9—11 кл.: От учебной задачи к творческой: Учебное пособие. — М.: Дрофа, 1996. — № 6, с. 5
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — с. 98
Источник: Калинин А. Ю., Терёшин Д. А. Геометрия. 10—11 классы. — М.: МЦНМО, 2011. — с. 590


