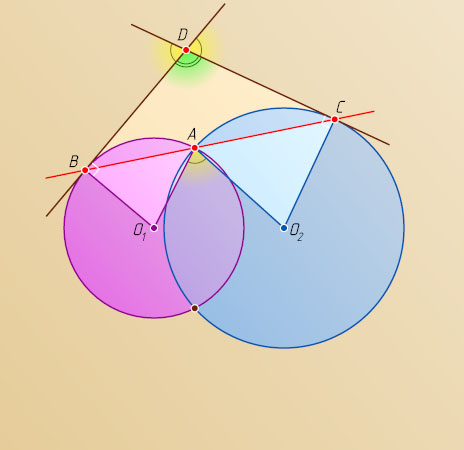
88. Окружности S_{1}
и S_{2}
пересекаются в точке A
. Через точку A
проведена прямая, пересекающая S_{1}
в точке B
, S_{2}
— в точке C
. В точках C
и B
проведены касательные к окружностям, пересекающиеся в точке D
. Докажите, что синус угла BDC
не зависит от выбора прямой, проходящей через точку A
.
Указание. Докажите, что \angle BDC=180^{\circ}-\angle O_{1}AO_{2}
.
Решение. Пусть O_{1}
и O_{2}
— центры окружностей. Рассмотрим случай, когда точка A
лежит на отрезке BC
. Тогда
\angle BDC=180^{\circ}-(\angle DBA+\angle DCA)=180^{\circ}-\frac{\angle BO_{1}A+\angle AO_{2}C}{2}=
=180^{\circ}-\frac{180^{\circ}-2\angle BAO_{1}+180^{\circ}-2\angle CAO_{2}}{2}=
=\angle BAO_{1}+\angle CAO_{2}=180^{\circ}-\angle O_{1}AO_{2}.
Если же точка A
лежит вне отрезка BC
, то аналогично получим, что \angle BDC=\angle O_{1}AO_{2}
. Отсюда следует утверждение задачи.
Примечание. Можно доказать, что точка D
лежит на кардиоиде (см. статью P. Pamfilos // Journal of Classical Geometry. Vol. 3 (2014). Pp. 12—34. Theorem 2).
Источник: Прасолов В. В. Задачи по планиметрии. — 6-е изд. — М.: МЦНМО, 2007. — № 2.26, с. 34

