89. Лемма Архимеда. Две окружности касаются внутренним образом в точке M
. Пусть AB
— хорда большей окружности, касающаяся меньшей окружности в точке T
. Докажите, что MT
— биссектриса угла AMB
.
Указание. Продолжите луч AB
до пересечения с общей касательной в точке C
; \angle CTM=\angle MAT+\angle AMT
(или рассмотрите гомотетию с центром M
, переводящую меньшую окружность в большую).
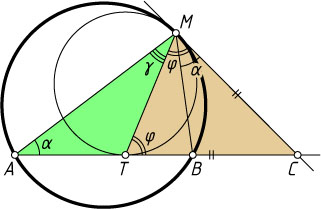
Решение. Первый способ. Пусть луч AB
(рис. 1) пересекает общую касательную к окружностям в точке C
(B
между A
и C
). Обозначим
\angle CMT=\varphi,~\angle CMB=\alpha,~\angle AMT=\gamma.
Тогда CM=CT
как отрезки касательных, проведённых к окружности из одной точки. Значит, треугольник MCT
— равнобедренный. Из теоремы об угле между касательной и хордой следует, что
\angle MAT=\angle CMB=\alpha.
Поэтому
\angle CTM=\angle CMT=\varphi,~\angle MTB=\alpha+\gamma=\varphi
(внешний угол треугольника AMT
). Следовательно,
\angle TMB=\varphi-\alpha=\gamma.
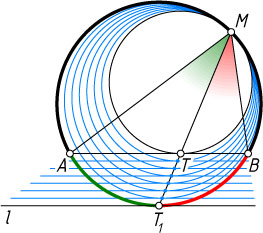
Второй способ. При гомотетии с центром M
, переводящей меньшую окружность в большую, касательная AB
к меньшей окружности переходит в параллельную ей касательную l
к большей окружности (рис. 2). Точка касания T
переходит в точку касания T_{1}
прямой l
с большей окружностью. Тогда точки M
, T
и T_{1}
лежат на одной прямой, причём T_{1}
делит пополам дугу AB
, не содержащую точки M
. Значит, вписанные углы AMT_{1}
и BMT_{1}
равны, так как они опираются на равные дуги. Следовательно, MT
— биссектриса угла AMB
.
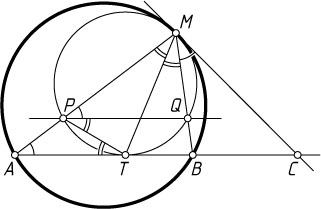
Третий способ. Пусть луч AB
(рис. 3) пересекает общую касательную к окружностям в точке C
(B
между A
и C
), а лучи MA
и MB
пересекают меньшую окружность в точках P
и Q
соответственно. Из теоремы об угле между касательной и хордой следует, что
\angle MAB=\angle MAT=\angle CMB=\angle CMQ=\angle MPQ,
значит, PQ\parallel AB
. Следовательно,
\angle BMT=\angle QPT=\angle ATP=\angle PMT=\angle AMT.
Что и требовалось доказать.
Источник: Всероссийская олимпиада школьников. — 1977-78, IV, III этап, 10 класс
Источник: Пржевальский Е. Собрание геометрических теорем и задач. — М.: Типография Г. Лисснера и Д. Собко, 1909. — № 70, с. 36
Источник: Прасолов В. В. Задачи по планиметрии. — Ч. 1. — М.: Наука, 1991. — № 2.27, с. 34
Источник: Прасолов В. В. Задачи по планиметрии. — 6-е изд. — М.: МЦНМО, 2007. — № 2.28, с. 34
Источник: Зарубежные математические олимпиады. — 1980, Люксембург
Источник: Конягин С. В. и др. Зарубежные математические олимпиады / Под ред. И. Н. Сергеева. — М.: Наука, 1987. — № 10.8, с. 34, Люксембург, 1980 г.
Источник: Понарин Я. П. Элементарная геометрия. — Т. 1: Планиметрия, преобразования плоскости. — М.: МЦНМО, 2004. — № 1.3, с. 16
Источник: Жижилкин И. Д. Инверсия. — (Библиотека «Математическое просвещение». Вып. 35). — М.: МЦНМО, 2009. — с. 22
Источник: Мерзляк А. Г., Поляков В. М. Геометрия. 9 класс. Углублённый уровень. — М.: Вентана-Граф, 2020. — № 23.55, с. 221
Источник: Кушнир И. А. Геометрия. Поиск и вдохновение. — М.: МЦНМО, 2013. — с. 492


