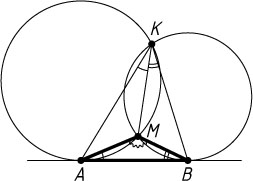
90. К двум окружностям, пересекающимся в точках K
и M
, проведена общая касательная. Докажите, что если A
и B
— точки касания, то сумма углов AMB
и AKB
равна 180^{\circ}
.
Указание. \angle AKM=\angle BAM
, \angle BKM=\angle ABM
.
Решение. Из теоремы об угле между касательной и хордой следует, что
\angle AKM=\angle BAM,~\angle BKM=\angle ABM,
следовательно,
\angle AMB+\angle AKB=\angle AMB+\angle BAM+\angle ABM=180^{\circ}.
Источник: Всероссийская олимпиада школьников. — 1987-88, XIV, IV этап, 9 класс
Источник: Журнал «Квант». — 1988, № 10, с. 56, задача 2
