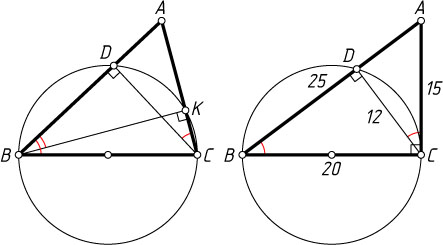
91. На стороне BC
треугольника ABC
как на диаметре построена окружность, пересекающая отрезок AB
в точке D
. Найдите отношение площадей треугольников ABC
и BCD
, если известно, что AC=15
, BC=20
и \angle ABC=\angle ACD
.
Ответ. \frac{25}{16}
.
Указание. Докажите, что треугольник ABC
— прямоугольный.
Решение. Если окружность пересекает сторону AC
в точке K
, то \angle KCD=\angle DBK
. Следовательно, \angle DBK=\angle DBC
. Значит, точка K
совпадает с точкой C
. Поэтому \angle ACB=90^{\circ}
и CD
— высота прямоугольного треугольника ACB
, проведённая из вершины прямого угла. Тогда
CD=\frac{AC\cdot BC}{AB}=12.
Треугольник ABC
подобен треугольнику CBD
с коэффициентом \frac{AB}{BC}=\frac{5}{4}
. Следовательно, их площади относятся как \left(\frac{5}{4}\right)^{2}
.
Источник: Вступительный экзамен на геологический факультет МГУ. — 1970, № 4, вариант 2
Источник: Гордин Р. К. ЕГЭ 2013. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2014. — № 7.35, с. 67
Источник: Гордин Р. К. ЕГЭ 2017. Математика. Геометрия. Стереометрия. Задача 14 (профильный уровень). — М.: МЦНМО, 2017. — № 7.35.1, с. 71
