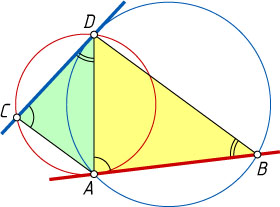
92. Даны две окружности, пересекающиеся в точках A
и D
; AB
и CD
— касательные к первой и второй окружностям (B
и C
— точки на окружностях). Докажите, что \frac{AC}{BD}=\frac{CD^{2}}{AB^{2}}
.
Указание. Треугольники DAC
и BDA
подобны.
Решение. Из теоремы об угле между касательной и хордой следует, что \angle BAD=\angle ACD
и \angle ABD=\angle ADC
. Поэтому треугольники DAC
и BDA
подобны. Следовательно,
\frac{AD}{DB}=\frac{CD}{AB},~\frac{AC}{AD}=\frac{CD}{AB}.
Перемножив почленно эти равенства, получим, что
\frac{AC}{BD}=\frac{CD^{2}}{AB^{2}}.
Источник: Шарыгин И. Ф. Задачи по геометрии. Планиметрия. — 2-е изд. — М.: Наука, 1986. — № 34, с. 10
Источник: Шарыгин И. Ф. Геометрия: 9—11 кл.: От учебной задачи к творческой: Учебное пособие. — М.: Дрофа, 1996. — № 34, с. 8
