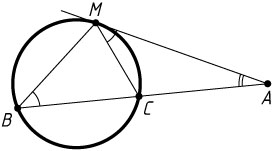
93. Теорема о касательной и секущей. Из одной точки проведены касательная и секущая к некоторой окружности. Докажите, что произведение всей секущей на её внешнюю часть равно квадрату длины отрезка касательной.
Указание. Воспользуйтесь теоремой об угле между касательной и хордой и рассмотрите подобные треугольники.
Решение. Пусть A
— данная точка вне окружности, AM
— касательная к этой окружности (M
— точка касания), ACB
— секущая, причём точка C
лежит между точками A
и B
.
Поскольку угол CMA
равен углу MBA
, то треугольники ABM
и AMC
подобны. Поэтому AM:AC=AB:AM
. Следовательно,
AC\cdot AB=AM^{2}.
