94. Из точки A
, лежащей вне окружности, проведены к окружности касательная и секущая. Расстояние от точки A
до точки касания равно 16, а расстояние от точки A
до одной из точек пересечения секущей с окружностью равно 32. Найдите радиус окружности, если расстояние от её центра до секущей равно 5.
Ответ. 13.
Указание. Примените теорему о касательной и секущей.
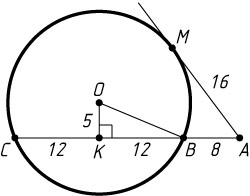
Решение. Пусть секущая пересекает окружность в точках B
и C
, а M
— точка касания. Тогда AM=16
, AC=32
, AB=32-BC
. По теореме о касательной и секущей
AM^{2}=AC\cdot AB,~\mbox{или}~16^{2}=32(32-BC).
Отсюда находим, что BC=24
.
Пусть K
— проекция центра O
данной окружности на хорду BC
. Радиус окружности находим по теореме Пифагора из прямоугольного треугольника OKB
:
R=OB=\sqrt{OK^{2}+BK^{2}}=\sqrt{25+144}=13.
Источник: Сборник задач по математике для поступающих во втузы / Под ред. М. И. Сканави. — 5-е изд. — М.: Высшая школа, 1988. — № 10.012, с. 159
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — с. 92
