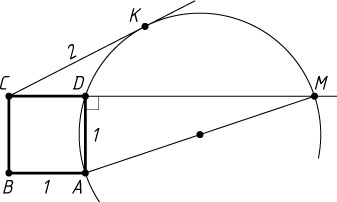
96. Сторона квадрата ABCD
равна 1 и является хордой некоторой окружности, причём остальные стороны квадрата лежат вне этой окружности. Касательная CK
, проведённая из вершины C
к этой же окружности, равна 2. Найдите диаметр окружности.
Ответ. \sqrt{10}
.
Указание. Примените теорему о касательной и секущей.
Решение. Пусть AD
— хорда окружности, луч CD
пересекает окружность в точке M
, отличной от D
. Тогда CM\cdot CD=CK^{2}
. Отсюда находим, что DM=3
.
Поскольку \angle ADM=90^{\circ}
, то AM
— диаметр окружности. По теореме Пифагора из прямоугольного треугольника ADM
находим, что
AM^{2}=AD^{2}+DM^{2}=1+9=10,~AM=\sqrt{10}.
Источник: Вступительный экзамен на геологический факультет МГУ. — 1973, вариант 1, № 3
Источник: Александров Б. И., Лурье М. В. Пособие по математике для поступающих в МГУ. — М.: Изд-во МГУ, 1977. — с. 52
Источник: Шарыгин И. Ф. Геометрия: 9—11 кл.: От учебной задачи к творческой: Учебное пособие. — М.: Дрофа, 1996. — № 97, с. 13
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — № 12.19, с. 94
