97. Окружность радиуса R
проходит через вершины A
и B
треугольника ABC
и касается прямой AC
в точке A
. Найдите площадь треугольника ABC
, зная, что \angle ABC=\beta
, \angle CAB=\alpha
.
Ответ. \frac{2R^{2}\sin^{3}\alpha\sin\beta}{\sin(\alpha+\beta)}
.
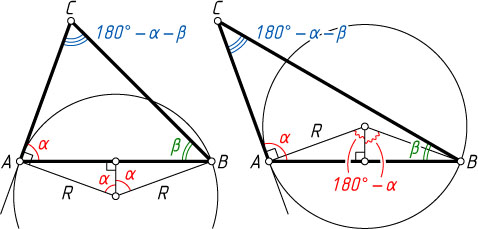
Указание. Сторона AB
видна из центра окружности под углом 2\alpha
или 360^{\circ}-2\alpha
.
Решение. Сторона AB
видна из центра окружности под углом 2\alpha
или 360^{\circ}-2\alpha
. Поэтому AB=2R\sin\alpha
. Из треугольника ABC
по теореме синусов находим, что
AC=\frac{AB\sin\beta}{\sin(180^{\circ}-\alpha-\beta)}=\frac{AB\sin\beta}{\sin(\alpha+\beta)}=\frac{2R\sin\alpha\sin\beta}{\sin(\alpha+\beta)}.
Следовательно,
S_{\triangle ABC}=\frac{1}{2}AB\cdot AC\sin\alpha=\frac{2R^{2}\sin^{3}\alpha\sin\beta}{\sin(\alpha+\beta)}.
Источник: Вступительный экзамен на географический факультет МГУ. — 1972, вариант 1, № 5
Источник: Александров Б. И., Лурье М. В. Пособие по математике для поступающих в МГУ. — М.: Изд-во МГУ, 1977. — с. 48
Источник: Понарин Я. П. Элементарная геометрия. — Т. 1: Планиметрия, преобразования плоскости. — М.: МЦНМО, 2004. — № 3.27, с. 33
