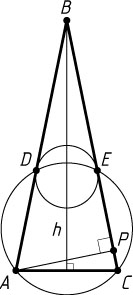
98. Окружность касается сторон AB
и BC
треугольника ABC
соответственно в точках D
и E
. Найдите высоту треугольника ABC
, опущенную из точки A
, если AB=5
, AC=2
, а точки A
, D
, E
, C
лежат на одной окружности.
Ответ. \frac{4\sqrt{6}}{5}
.
Указание. Треугольник ABC
— равнобедренный.
Решение. По теореме о касательной и секущей BA\cdot BD=BE\cdot BC
. Поскольку BD=BE
, то AB=BC
, т. е. треугольник ABC
— равнобедренный.
Пусть h
— высота треугольника ABC
, опущенная из вершины B
. Тогда
h=\sqrt{AB^{2}-\left(\frac{AC}{2}\right)^{2}}=\sqrt{25-1}=2\sqrt{6}.
Если AP
— высота треугольника ABC
, то AC\cdot h=BC\cdot AP
. Следовательно,
AP=\frac{AC\cdot h}{BC}=\frac{2\cdot2\sqrt{6}}{5}=\frac{4\sqrt{6}}{5}.
Источник: Вступительный экзамен на механико-математический факультет МГУ. — 1981, вариант 1, № 3
Источник: Нестеренко Ю. В., Олехник С. Н., Потапов М. К. Задачи вступительных экзаменов по математике. — М.: Факториал, 1995. — с. 8
Источник: Кюршак Й. и др. Венгерские математические олимпиады. — М.: Мир, 1976. — с. 502
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — № 5.21, с. 40
