99. Из точки A
проведены секущая и касательная к окружности радиуса R
. Пусть B
— точка касания, а D
и C
— точки пересечения секущей с окружностью, причём точка D
лежит между A
и C
. Известно, что BD
— биссектриса угла B
треугольника ABC
, и её длина равна R
. Найдите расстояние от точки A
до центра окружности.
Ответ. \frac{R\sqrt{7}}{2}
.
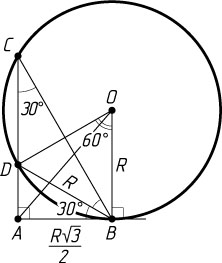
Указание. Докажите, что угол BAD
— прямой.
Решение. Поскольку BD=R
, то \angle BCD=30^{\circ}
. Тогда
\angle ABD=\angle BCD=30^{\circ},~\angle ABC=2\angle ABD=60^{\circ}.
Следовательно,
\angle BAC=90^{\circ},~AB=BD\cos30^{\circ}=\frac{R\sqrt{3}}{2}.
Если O
— центр окружности, то
OA=\sqrt{AB^{2}+OB^{2}}=\sqrt{\frac{3R^{2}}{4}+R^{2}}=\frac{R\sqrt{7}}{2}.
Источник: Вступительный экзамен на физический факультет МГУ. — 1969, № 4, вариант 1
Источник: Гордин Р. К. ЕГЭ 2013. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2014. — № 12.38, с. 118
Источник: Гордин Р. К. ЕГЭ 2017. Математика. Геометрия. Стереометрия. Задача 14 (профильный уровень). — М.: МЦНМО, 2017. — № 12.38.1, с. 128
