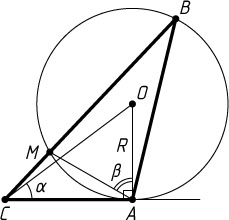
100. Окружность радиуса R
с центром в точке O
проходит через вершины A
и B
треугольника ABC
, пересекает отрезок BC
в точке M
и касается прямой AC
в точке A
. Найдите CM
, зная, что \angle ACO=\alpha
, \angle MAB=\beta
.
Ответ. R\left(\sqrt{\sin^{2}\beta+\ctg^{2}\alpha}-\sin\beta\right)
.
Указание. Примените теорему о касательной и секущей.
Решение. По теореме о касательной и секущей
AC^{2}=BC\cdot CM=(BM+CM)CM.
Поскольку BM=2R\sin\beta
и AC=R\ctg\alpha
, то
R^{2}\ctg^{2}\alpha=CM^{2}+CM\cdot2R\sin\beta,
или
CM^{2}+2R\sin\beta\cdot CM-R^{2}\ctg^{2}\alpha=0
Из этого уравнения находим, что
CM=R\left(\sqrt{\sin^{2}\beta+\ctg^{2}\alpha}-\sin\beta\right).
Источник: Вступительный экзамен на географический факультет МГУ. — 1972, вариант 2, № 5
Источник: Александров Б. И., Лурье М. В. Пособие по математике для поступающих в МГУ. — М.: Изд-во МГУ, 1977. — с. 49
