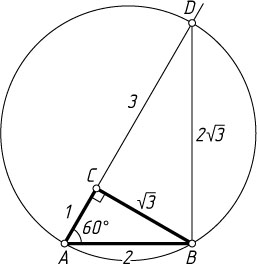
101. Гипотенуза AB
прямоугольного треугольника ABC
равна 2 и является хордой некоторой окружности. Катет AC
равен 1 и лежит внутри окружности, а его продолжение пересекает окружность в точке D
, причём CD=3
. Найдите радиус окружности.
Ответ. 2.
Указание. Примените формулу a=2R\sin\alpha
.
Решение. Из прямоугольных треугольников ABC
и BCD
находим, что
\angle BAC=60^{\circ},~BD=\sqrt{CD^{2}+BC^{2}}=2\sqrt{3}.
Если R
— искомый радиус, то
R=\frac{BD}{2\sin\angle BAC}=\frac{2\sqrt{3}}{2\sin60^{\circ}}=\frac{2\sqrt{3}}{\sqrt{3}}=2.
Источник: Вступительный экзамен на географический факультет МГУ. — 1973, вариант 2, № 3
Источник: Александров Б. И., Лурье М. В. Пособие по математике для поступающих в МГУ. — М.: Изд-во МГУ, 1977. — с. 53
