102. Сторона AB
правильного шестиугольника ABCDEF
равна \sqrt{3}
и является хордой некоторой окружности, причём остальные стороны шестиугольника лежат вне этой окружности. Длина касательной CM
, проведённой к той же окружности из вершины C
(соседней с вершиной B
), равна 3. Найдите диаметр окружности.
Ответ. 2\sqrt{3}
.
Указание. Докажите, что прямая BC
проходит через центр данной окружности.
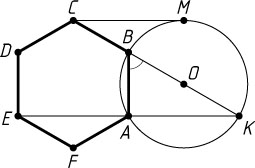
Решение. Пусть M
— точка касания, K
— вторая точка пересечения прямой BC
с данной окружностью. Тогда CK\cdot CB=CM^{2}
. Отсюда находим, что CK=3\sqrt{3}
, BK=CK-BC=2\sqrt{3}
. В треугольнике ABK
известно, что
AB=\sqrt{3},~BK=2\sqrt{3}=2AB,~\angle ABK=180^{\circ}-\angle ABC=180^{\circ}-120^{\circ}=60^{\circ}.
Значит, треугольник ABK
— прямоугольный, BK
— его гипотенуза. Следовательно, BK=2\sqrt{3}
— искомый диаметр.
Источник: Вступительный экзамен на географический факультет МГУ. — 1973, вариант 3, № 3
Источник: Александров Б. И., Лурье М. В. Пособие по математике для поступающих в МГУ. — М.: Изд-во МГУ, 1977. — с. 54
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — Диагностическая работа 2, задача 4
Источник: Гордин Р. К. ЕГЭ 2017. Математика. Геометрия. Стереометрия. Задача 14 (профильный уровень). — М.: МЦНМО, 2017. — № 4, с. 165
