103. Сторона AB
треугольника ABC
является хордой некоторой окружности. Стороны AC
и BC
лежат внутри окружности, продолжение стороны AC
пересекает окружность в точке D
, а продолжение стороны BC
— в точке E
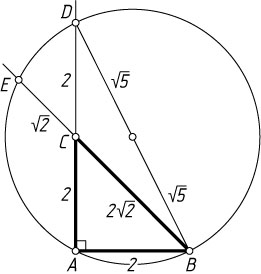
, причём AB=AC=CD=2
, CE=\sqrt{2}
. Найдите радиус окружности.
Ответ. \sqrt{5}
.
Указание. Докажите, что угол BAC
— прямой.
Решение. По теореме о произведении отрезков пересекающихся хорд BC\cdot CE=AC\cdot CD
. Отсюда находим, что
BC=\frac{AC\cdot CD}{CE}=2\sqrt{2}.
Из треугольника ABC
находим, что угол BAC
— прямой. Поэтому DB
— диаметр окружности и
DB=\sqrt{AB^{2}+AD^{2}}=\sqrt{20}=2\sqrt{5}.
Источник: Вступительный экзамен на географический факультет МГУ. — 1973, вариант 4, № 3
Источник: Александров Б. И., Лурье М. В. Пособие по математике для поступающих в МГУ. — М.: Изд-во МГУ, 1977. — с. 54
