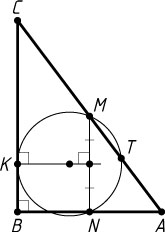
104. В прямоугольном треугольнике ABC
с катетами AB=3
и BC=4
через середины сторон AB
и AC
проведена окружность, касающаяся катета BC
. Найдите длину отрезка гипотенузы AC
, который лежит внутри этой окружности.
Ответ. \frac{11}{10}
.
Указание. Примените теорему о касательной и секущей.
Решение. Пусть M
и N
— середины AC
и AB
соответственно, K
— точка касания. Тогда MN
— средняя линия треугольника ABC
; диаметр окружности, проходящий через точку касания K
, перпендикулярен BC
, а значит, и MN
. Поэтому
MN=\frac{1}{2}BC=2,~CK=CB-KB=CB-\frac{1}{2}MN=4-1=3.
Пусть T
— вторая точка пересечения окружности с гипотенузой AC
. Тогда
CT\cdot CM=CK^{2},~\mbox{или}~\left(\frac{5}{2}+MT\right)\frac{5}{2}=9.
Отсюда находим, что MT=\frac{11}{10}
.
Источник: Вступительный экзамен на географический факультет МГУ. — 1971, № 4, вариант 1
Источник: Шарыгин И. Ф. Геометрия: 9—11 кл.: От учебной задачи к творческой: Учебное пособие. — М.: Дрофа, 1996. — № 132, с. 16
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — № 12.20, с. 94
