105. Окружность касается сторон AB
и AD
прямоугольника ABCD
и проходит через вершину C
. Сторону DC
она пересекает в точке N
. Найдите площадь трапеции ABND
, если AB=9
и AD=8
.
Ответ. 40.
Указание. Обозначьте DN=x
и примените теорему о касательной и секущей.
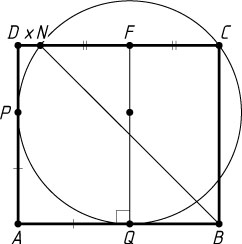
Решение. Обозначим DN=x
. Пусть P
и Q
— точки касания окружности со сторонами соответственно AD
и AB
данного прямоугольника, а перпендикуляр к стороне AB
, проведённый через точку Q
, пересекает сторону DC
в точке F
. Тогда центр окружности лежит на прямой QF
, а так как диаметр, перпендикулярный хорде, делит её пополам, то F
— середина хорды CN
.
По теореме о касательной и секущей PD^{2}=DC\cdot DN=9x
, поэтому PD=3\sqrt{x}
. Тогда
AQ=AP=AD-PD=8-3\sqrt{x}=AQ,~QB=AB-AQ=9-(8-3\sqrt{x})=1+3\sqrt{x},~
NC=2CF=2QB=2+6\sqrt{x}.
Поскольку NC+ND=9
, то
2+6\sqrt{x}+x=9,~\mbox{или}~x+6\sqrt{x}-7=0.
Отсюда находим, что x=1.
Следовательно,
S_{ABND}=\frac{AB+ND}{2}\cdot AD=10\cdot4=40.
