106. Две окружности радиусов r
и R
(r\lt R
) касаются друг друга внешним образом. Прямая касается этих окружностей в точках M
и N
. В точках A
и B
окружности касаются внешним образом третьей окружности. Прямые AB
и MN
пересекаются в точке C
. Из точки C
проведена касательная к третьей окружности (D
— точка касания). Найдите CD
.
Ответ. \frac{2rR}{R-r}
.
Указание. 1) Докажите, что прямые MN
и AB
пересекаются на прямой, проходящей через центры двух первых окружностей.
2) Докажите, что CD=CP
, где P
— точка касания двух первых окружностей.
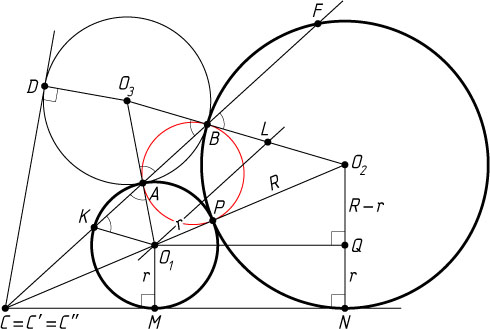
Решение. Пусть O_{1}
и O_{2}
— центры окружностей радиусов r
и R
соответственно, O_{3}
— центр третьей окружности, K
— вторая точка пересечения прямой AC
с первой окружностью, P
— точка касания двух первых окружностей.
Поскольку эти окружности касаются, то точка P
лежит на прямой O_{1}O_{2}
. Докажем, что точка пересечения прямых MN
и AB
также лежит на прямой O_{1}O_{2}
.
Пусть прямая MN
пересекает прямую O_{1}O_{2}
в точке C'
. Если Q
— проекция точки O_{1}
на O_{2}N
, то треугольник O_{1}MC'
подобен треугольнику O_{2}QO_{1}
с коэффициентом
\frac{O_{1}M}{O_{2}Q}=\frac{O_{1}M}{O_{2}N-NQ}=\frac{O_{1}M}{O_{2}N-O_{1}M}=\frac{r}{R-r}.
Поэтому
C'O_{1}=\frac{r}{R-r}\cdot O_{1}O_{2}=\frac{r}{R-r}\cdot(R+r)=\frac{r(R+r)}{R-r}.
Пусть прямая AB
пересекает прямую O_{1}O_{2}
в точке C''
. Поскольку точка A
лежит на отрезке O_{1}O_{3}
, а точка B
— на O_{2}O_{3}
, то
\angle O_{1}KA=\angle O_{1}AK=\angle O_{3}AB=\angle O_{3}BA=\angle O_{2}BF,
где F
— вторая точка пересечения прямой AB
и окружности с центром O_{2}
. Поэтому KO_{1}\parallel BO_{2}
. Пусть прямая, проходящая через точку O_{1}
параллельно AB
, пересекает радиус O_{2}B
в точке L
. Тогда треугольник O_{1}KC''
подобен треугольнику O_{2}LO_{1}
с коэффициентом
\frac{O_{1}K}{O_{2}L}=\frac{O_{1}K}{O_{2}B-BL}=\frac{O_{1}K}{O_{2}B-O_{1}K}=\frac{r}{R-r}.
Поэтому
C''O_{1}=\frac{r}{R-r}\cdot O_{1}O_{2}=\frac{r}{R-r}\cdot(R+r)=\frac{r(R+r)}{R-r}.
Таким образом, C'O_{1}=C''O_{1}
. Значит, точки C'
и C''
совпадают. Следовательно, прямые MN
и AB
пересекаются на прямой O_{1}O_{2}
.
Теперь найдём CD
. Для этого сначала заметим, что точки A
, P
и B
на сторонах треугольника O_{1}O_{2}O_{3}
таковы, что
O_{1}A=O_{1}P,~O_{2}B=O_{2}P,~O_{3}A=O_{3}B.
Значит, в этих точках вписанная окружность треугольника O_{1}O_{2}O_{3}
касается его сторон (см. задачу 4728). Поскольку CP
— касательная к этой окружности, CD
— касательная к окружности с центром O_{3}
, а CAB
— общая секущая этих окружностей, то
CD^{2}=CA\cdot CB=CP^{2}
Следовательно,
CD=CP=CO_{1}+O_{1}P=\frac{r(R+r)}{R-r}+r=\frac{2rR}{R-r}.
Источник: Вступительный экзамен на физический факультет МГУ. — 1984, вариант 2, № 6
Источник: Нестеренко Ю. В., Олехник С. Н., Потапов М. К. Задачи вступительных экзаменов по математике. — М.: Наука, 1986. — с. 504
Источник: Нестеренко Ю. В., Олехник С. Н., Потапов М. К. Задачи вступительных экзаменов по математике. — М.: Факториал, 1995. — с. 38
Источник: Шарыгин И. Ф. Геометрия: 9—11 кл.: От учебной задачи к творческой: Учебное пособие. — М.: Дрофа, 1996. — № 683, с. 86
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — № 9.48, с. 71
