107. Каждая из боковых сторон AB
и BC
равнобедренного треугольника ABC
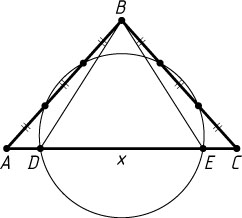
разделена на три равные части, и через четыре точки деления на этих сторонах проведена окружность, высекающая на основании AC
хорду DE
. Найдите отношение площадей треугольников ABC
и BDE
, если AB=BC=3
и AC=4
.
Ответ. \sqrt{2}
.
Указание. Произведение всей секущей на её внешнюю часть для данной точки и данной окружности постоянно.
Решение. Поскольку треугольник ABC
— равнобедренный, то AD=EC
. Обозначим DE=x
. Тогда
CE=\frac{4-x}{2},~CD=\frac{4+x}{2}.
Из точки C
к указанной окружности проведены две секущие. Произведение всей секущей на её внешнюю часть данной точки и данной окружности постоянно. Поэтому
CE\cdot CD=2,~\mbox{или}~\frac{16-x^{2}}{4}=2.
Отсюда находим, что x=2\sqrt{2}
. Следовательно,
\frac{S_{\triangle ABC}}{S_{\triangle BDE}}=\frac{AC}{DE}=\frac{4}{2\sqrt{2}}=\sqrt{2}.
Источник: Вступительный экзамен на географический факультет МГУ. — 1972, № 4, вариант 2
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — № 12.14, с. 94
