108. В треугольнике ABC
известно, что AB=\sqrt{14}
и BC=2
. Окружность проведена через точку B
, через середину D
отрезка BC
, через точку E
на отрезке AB
и касается стороны AC
. Найдите отношение, в котором эта окружность делит отрезок AB
, если DE
— диаметр этой окружности.
Ответ. 4:3
.
Указание. Примените теорему о касательной и секущей.
Решение. Поскольку ED
— диаметр окружности, то \angle B=90^{\circ}
. Поэтому
AC=\sqrt{BC^{2}+AB^{2}}=3\sqrt{2}.
Пусть P
— точка касания окружности с гипотенузой AC
. Тогда
PC^{2}=CB\cdot CD=2,~PC=\sqrt{2},~AP=3\sqrt{2}-\sqrt{2}=2\sqrt{2},
AB\cdot AE=AP^{2},~\mbox{или}\sqrt{14}(\sqrt{14}-BE)=8.
Отсюда находим, что
BE=\frac{3\sqrt{14}}{7},~AE=\sqrt{14}-\frac{3\sqrt{14}}{7}=\frac{4\sqrt{14}}{7},~\frac{AE}{BE}=\frac{4}{3}.
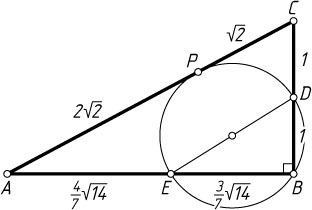
Источник: Вступительный экзамен на географический факультет МГУ. — 1971, № 4, вариант 3
