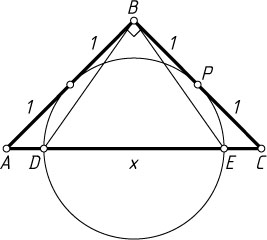
109. В равнобедренном треугольнике ABC
угол B
— прямой, а AB=BC=2
. Окружность касается обоих катетов в их серединах и высекает на гипотенузе хорду DE
. Найдите площадь треугольника BDE
.
Ответ. \sqrt{2}
.
Решение. Пусть точка E
лежит между точками D
и C
. Обозначим DE=x
; P
— точка касания окружности с катетом BC
.
Поскольку CD\cdot CE=CP^{2}
, то
\left(\sqrt{2}+\frac{x}{2}\right)\left(\sqrt{2}-\frac{x}{2}\right)=1.
Отсюда находим, что x=2
. Следовательно,
S_{\triangle BDE}=\frac{DE}{AC}S_{\triangle ABC}=\sqrt{2}.
Источник: Вступительный экзамен на географический факультет МГУ. — 1971, № 4, вариант 4
