110. Центр окружности, касающейся стороны BC
треугольника ABC
в точке B
и проходящей через точку A
, лежит на отрезке AC
. Найдите площадь треугольника ABC
, если известно, что BC=6
и AC=9
.
Ответ. \frac{135}{13}
.
Указание. Примените теорему о касательной и секущей.
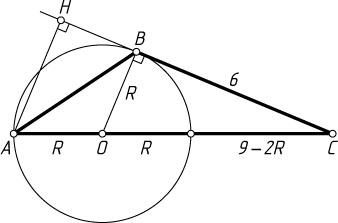
Решение. Пусть R
— радиус окружности. Тогда
(AC-2R)AC=BC^{2}.
Отсюда находим, что R=\frac{5}{2}
.
Пусть H
— основание высоты, опущенной из точки A
, O
— центр окружности. Тогда \frac{AH}{OB}=\frac{AC}{CO}
. Поэтому
AH=\frac{AC\cdot OB}{CO}=\frac{AC\cdot R}{AC-R}=\frac{45}{13}.
Следовательно,
S_{\triangle ABC}=\frac{1}{2}BC\cdot AH=\frac{135}{13}.
Источник: Вступительный экзамен на географический факультет МГУ. — 1969, № 4, вариант 1
