111. Медианы AM
и BE
треугольника ABC
пересекаются в точке O
. Точки O
, M
, E
, C
лежат на одной окружности. Найдите AB
, если BE=AM=3
.
Ответ. 2\sqrt{3}
.
Указание. Докажите, что треугольник ABC
— равносторонний.
Решение. Поскольку OE=\frac{1}{3}BE
и OM=\frac{1}{3}AM
, то OE=OM
. Поэтому CO
— биссектриса угла ECM
.
Из равенства медиан BE
и AM
следует, что треугольник ABC
— равнобедренный. Поэтому EC=CM
. Тогда треугольники CEO
и CMO
равны, а так как
\angle CEO+\angle CMO=180^{\circ},
то
\angle CEO=\angle CMO=90^{\circ},
т. е. медианы AM
и BE
являются высотами. Поэтому треугольник ABC
— равносторонний. Следовательно,
AB=\frac{AM}{\sin60^{\circ}}=2\sqrt{3}.
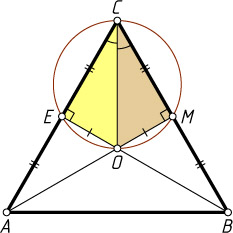
Источник: Вступительный экзамен на филологический факультет МГУ. — 1987, вариант 1, № 4
Источник: Нестеренко Ю. В., Олехник С. Н., Потапов М. К. Задачи вступительных экзаменов по математике. — М.: Факториал, 1995. — с. 183
