112. С помощью циркуля и линейки постройте окружность, проходящую через две данные точки и касающуюся данной прямой.
Указание. Примените теорему о касательной и секущей.
Решение. Первый способ. Пусть A
и B
— данные точки, M
— точка пересечения прямой AB
с данной прямой, K
— искомая точка касания. По теореме о касательной и секущей MK=\sqrt{MB\cdot MA}
.
Отсюда вытекает следующий способ построения. Строим отрезок, равный среднему геометрическому известных отрезков MB
и MA
, и откладываем его по разные стороны от точки M
на данной прямой. Пусть MP
— один из таких отрезков. Опишем окружность около треугольника ABP
. Докажем, что эта окружность — искомая. Действительно, по построению она проходит через точки A
и B
и, кроме того, MP^{2}=MA\cdot MB
. Если P_{1}
— ещё одна общая точка данной прямой и построенной окружности, то
MP\cdot(MP\pm PP_{1})=MA\cdot MB=MP^{2},
поэтому точки P
и P_{1}
совпадают. Следовательно, окружность, проходящая через точки A
, B
и P
, касается данной прямой. Аналогично для второго отрезка.
Если точки A
и B
расположены по одну сторону от данной прямой и удалены от неё на разные расстояния, то задача имеет два решения, если на равные — одно решение. В остальных случаях решений нет.
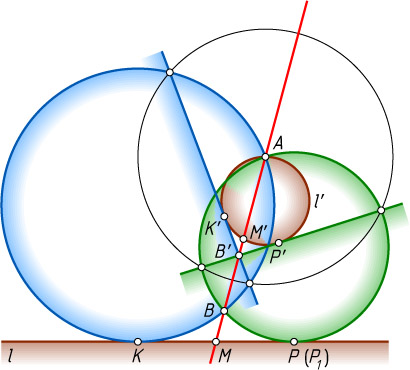
Второй способ. Пусть A
и B
— данные точки, l
— данная прямая, K
— искомая точка касания. Рассмотрим случай, когда ни A
, ни B
не лежат на прямой l
.
При инверсии относительно произвольной окружности с центром A
, прямая AB
, проходящая через центр инверсии, перейдёт в себя, точка B
перейдёт в точку B'
, лежащую на этой прямой, прямая l
, не проходящая через центр инверсии, — в окружность l'
, проходящую через центр инверсии, т. е. через точку A
, а искомая окружность — в прямую, касающуюся окружности l'
.
Заметим, что точку B'
и окружность l'
можно построить с помощью циркуля и линейки, так как можно построить образ любой точки при инверсии относительно любой окружности.
Если точка B'
не лежит внутри окружности l'
, то проведём через точку B'
касательную к этой окружности. При рассматриваемой инверсии эта касательная перейдёт в окружность, проходящую через точки A
и B
и касающуюся прямой l'
.
Если точка B'
лежит внутри окружности l'
, задача не имеет решений. Если точка B'
лежит на окружности l'
, задача имеет единственное решение. Если точка B'
лежит вне окружности l'
, задача имеет ровно два решения.
Источник: Адамар Ж. Элементарная геометрия. — Ч. 1: Планиметрия. — М.: Учпедгиз, 1948. — с. 151
Источник: Яглом И. М. Геометрические преобразования. — Т. 2: Линейные и круговые преобразования. — М.: ГИТТЛ, 1956. — № 232(а), с. 207; № 247(а), с. 230
Источник: Делоне Б. Н., Житомирский О. К. Задачник по геометрии. — М.—Л.: ОГИЗ, 1949. — № 185, с. 20
Источник: Пойа Д. Математическое открытие. — М.: Наука, 1970. — № 41, с. 40
Источник: Прасолов В. В. Задачи по планиметрии. — Ч. 2. — М.: Наука, 1991. — № 28.9, с. 186
Источник: Прасолов В. В. Задачи по планиметрии. — 6-е изд. — М.: МЦНМО, 2007. — № 28.10, с. 519
Источник: Понарин Я. П. Элементарная геометрия. — Т. 1: Планиметрия, преобразования плоскости. — М.: МЦНМО, 2004. — № 2.17, с. 24
