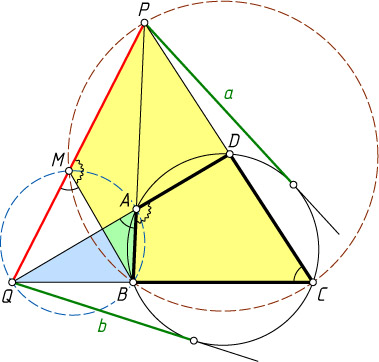
116. Противоположные стороны четырёхугольника, вписанного в окружность, пересекаются в точках P
и Q
. Найдите PQ
, если касательные к окружности, проведённые из точек P
и Q
, равны a
и b
.
Ответ. \sqrt{a^{2}+b^{2}}
.
Указание. Примените теорему о касательной и секущей.
Решение. Пусть DA
и CB
пересекаются в точке Q
, BA
и CD
— в точке P
, а окружность, описанная около треугольника ABQ
, пересекает отрезок PQ
в точке M
.
Поскольку
\angle BMP=180^{\circ}-\angle BMQ=180^{\circ}-\angle BAQ=180^{\circ}-\angle BCD=180^{\circ}-\angle BCP,
то около четырёхугольника CBMP
можно описать окружность. Тогда
QM\cdot QP=QC\cdot QB=QA\cdot QD=b^{2},~PM\cdot PQ=PA\cdot PB=PC\cdot PD=a^{2}.
Сложив почленно эти равенства, получим, что
a^{2}+b^{2}=QM\cdot QP+PM\cdot PQ=PQ(QM+PM)=PQ^{2}.
Источник: Пржевальский Е. Собрание геометрических теорем и задач. — М.: Типография Г. Лисснера и Д. Собко, 1909. — № 235, с. 96
Источник: Шарыгин И. Ф. Задачи по геометрии. Планиметрия. — 2-е изд. — М.: Наука, 1986. — № 271, с. 32
Источник: Шарыгин И. Ф. Геометрия: 9—11 кл.: От учебной задачи к творческой: Учебное пособие. — М.: Дрофа, 1996. — № 271, с. 31
