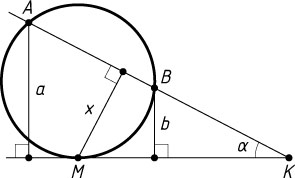
117. Окружность и прямая касаются в точке M
. Из точек A
и B
этой окружности опущены перпендикуляры на прямую, равные a
и b
соответственно. Найдите расстояние от точки M
до прямой AB
.
Ответ. \sqrt{ab}
.
Указание. Примените теорему о касательной и секущей.
Решение. Если прямая AB
параллельна касательной, то всё очевидно.
Пусть указанная касательная и прямая AB
пересекаются в точке K
под углом \alpha
, а x
— искомый отрезок. Тогда
\sin\alpha=\frac{b}{BK}=\frac{x}{MK}=\frac{a}{AK}.
Перемножив почленно равенства
\frac{a}{AK}=\frac{x}{MK},~\frac{b}{BK}=\frac{x}{MK},
получим:
\frac{ab}{AK\cdot BK}=\frac{x^{2}}{MK^{2}}.
Поскольку AK\cdot BK=MK^{2}
, то x^{2}=ab
. Следовательно, x=\sqrt{ab}
.
Источник: Вступительный экзамен в МИРЭА. —
Источник: Делоне Б. Н., Житомирский О. К. Задачник по геометрии. — М.—Л.: ОГИЗ, 1949. — № 176, с. 19
Источник: Моденов П. С. Сборник задач по специальному курсу элементарной математики. — М.: Советская наука, 1957. — № 39, с. 202
Источник: Прасолов В. В. Задачи по планиметрии. — Ч. 1. — М.: Наука, 1991. — № 2.52, с. 36
Источник: Прасолов В. В. Задачи по планиметрии. — 6-е изд. — М.: МЦНМО, 2007. — № 2.55, с. 36
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — № 12.30, с. 95
Источник: Понарин Я. П. Элементарная геометрия. — Т. 1: Планиметрия, преобразования плоскости. — М.: МЦНМО, 2004. — № 2.12, с. 24
