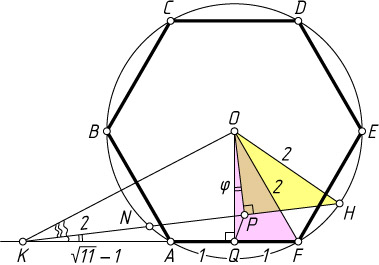
118. В окружность радиуса 2 вписан правильный шестиугольник ABCDEF
. Из точки K
, лежащей на продолжении стороны AF
так, что KA\lt KF
и KA=\sqrt{11}-1
, проведена секущая KH
, пересекающая окружность в точках N
и H
. Известно, что внешняя часть секущей KN
равна 2 (KN=2)
, а угол NFH
— тупой. Найдите угол HKF
.
Ответ. \arccos\frac{37}{2(7\sqrt{11}-\sqrt{21})}=\arccos\frac{7\sqrt{11}+\sqrt{21}}{28}=\arcsin\frac{7\sqrt{3}-\sqrt{77}}{28}
.
Указание. KA\cdot FK=KN\cdot KH
.
Решение. Первый способ. Пусть O
— центр окружности; P
, Q
— середины хорд NH
и AF
. Поскольку KA\cdot FK=KN\cdot KH
, то
(\sqrt{11}-1)(\sqrt{11}+1)=2(2+NH).
Отсюда находим, что NH=3
, KH=KN+NH=5
.
Из прямоугольных треугольников HPO
и FQO
находим, что
OP=\sqrt{OH^{2}-PH^{2}}=\sqrt{4-\frac{9}{4}}=\frac{\sqrt{7}}{2},
OQ=\sqrt{OA^{2}-AQ^{2}}=\sqrt{4-1}=\sqrt{3},
Выразим с помощью теоремы косинусов отрезок PQ
из треугольников KPQ
и OPQ
и решим полученное уравнение относительно косинуса искомого угла.
Обозначим \angle PKQ=\angle POQ=\varphi
. Тогда
KP^{2}+KQ^{2}-2KP\cdot KQ\cos\varphi=OP^{2}+OQ^{2}-2OP\cdot OQ\cos\varphi.
Следовательно,
\cos\varphi=\frac{KP^{2}+KQ^{2}-OP^{2}-OQ^{2}}{2(KP\cdot KQ-OP\cdot OQ)}=
=\frac{\frac{49}{4}+11-\frac{7}{4}-3}{2\left(\frac{7}{2}\cdot\sqrt{11}-\frac{\sqrt{7}}{2}\cdot\sqrt{3}\right)}=\frac{37}{2(7\sqrt{11}-\sqrt{21})}=\frac{7\sqrt{11}+\sqrt{21}}{28}.
Второй способ. Пусть O
— центр окружности; P
, Q
— середины хорд NH
и AF
. Поскольку KA\cdot FK=KN\cdot KH
, то
(\sqrt{11}-1)(\sqrt{11}+1)=2(2+NH).
Отсюда находим, что NH=3
, KH=KN+NH=5
. Далее последовательно находим:
OP=\sqrt{OH^{2}-PH^{2}}=\sqrt{4-\frac{9}{4}}=\frac{\sqrt{7}}{2},
OQ=\sqrt{OA^{2}-AQ^{2}}=\sqrt{4-1}=\sqrt{3},
OK=\sqrt{OQ^{2}+KQ^{2}}=\sqrt{3+11}=\sqrt{14},
\sin\angle QKO=\frac{OQ}{OK}=\frac{\sqrt{3}}{\sqrt{14}},~\sin\angle PKO=\frac{OP}{OK}=\frac{1}{2\sqrt{2}},
\cos\angle QKO=\frac{\sqrt{11}}{\sqrt{14}},~\cos\angle PKO=\frac{\sqrt{7}}{2\sqrt{2}}.
Следовательно,
\sin\angle HKF=\sin(\angle QKO-\angle PKO)=
=\frac{\sqrt{3}}{\sqrt{14}}\cdot\frac{\sqrt{7}}{2\sqrt{2}}-\frac{1}{2\sqrt{2}}\cdot\frac{\sqrt{11}}{\sqrt{14}}=\frac{7\sqrt{3}-\sqrt{77}}{28}.
Источник: Вступительный экзамен на биологический факультет МГУ. — 1989, вариант 1, № 4
Источник: Нестеренко Ю. В., Олехник С. Н., Потапов М. К. Задачи вступительных экзаменов по математике. — М.: Факториал, 1995. — с. 81
