120. Из точки M
, лежащей вне окружности, проведены к этой окружности две касательные. Расстояния от точки C
, лежащей на окружности, до касательных равны a
и b
. Найдите расстояние от точки C
до прямой AB
, где A
и B
— точки касания.
Ответ. \sqrt{ab}
.
Указание. Пусть x
— искомый отрезок. Рассмотрите подобные треугольники, среди сторон которых есть a
, b
и x
.
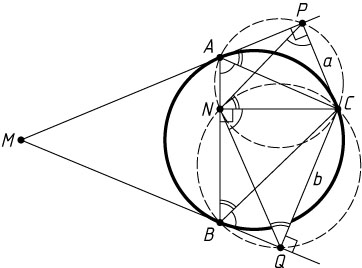
Решение. Пусть P
, Q
, N
— основания перпендикуляров, опущенных из точки C
на прямые MA
, MB
, AB
соответственно. Докажем, что треугольник PCN
подобен треугольнику NCQ
.
Действительно, отрезок AC
виден из точек P
и N
под прямым углом. Значит, точки P
и N
лежат на окружности с диаметром AC
. Точки N
и Q
лежат на окружности с диаметром BC
. Поэтому \angle CPN=\angle CAN=\angle CAB
, а из теоремы об угле между касательной и хордой следует, что \angle CAB=\angle CBQ=\angle CNQ
. Аналогично \angle CNP=\angle CQN
. Значит, треугольники PCN
и NCQ
подобны по двум углам. Следовательно, \frac{CN}{CQ}=\frac{CP}{CN}
. Поэтому
CN^{2}=CP\cdot CQ=ab.
Источник: Санкт-Петербургская (Ленинградская) математическая олимпиада. — 1934, третий тур, задача 7(б), 10 класс
Источник: Журнал «Квант». — 2020, № 7, с. 20
Источник: Пржевальский Е. Собрание геометрических теорем и задач. — М.: Типография Г. Лисснера и Д. Собко, 1909. — № 169, с. 89
Источник: Московская математическая олимпиада. — 1952, XV, 2-й тур, 8 класс
Источник: Моденов П. С. Сборник задач по специальному курсу элементарной математики. — М.: Советская наука, 1957. — № 2, с. 199; № 18, с. 201
Источник: Гальперин Г. А., Толпыго А. К. Московские математические олимпиады. — М.: Просвещение, 1988. — № 24, с. 42
Источник: Вступительный экзамен в МФТИ. — 1959, билет 4, № 3
Источник: Сборник методических материалов письменных испытаний по математике и физике абитуриентов Московского Физтеха (1947—2006 гг.). Математика / Сост. Д. А. Александров, И. Г. Почернин, И. Г. Проценко, И. Е. Сидорова, В. Б. Трушин, И. Г. Шомполов. Под ред. И. Г. Шомполова. — М.: МФТИ, 2007. — № 59-4-3, с. 71
Источник: Коксетер Г. С. М., Грейтцер С. Л. Новые встречи с геометрией. — М.: Наука, 1978. — № 4, с. 55
Источник: Устный вступительный экзамен в МФТИ. — 1977
Источник: Вступительный экзамен на физический факультет МГУ. — 1993, № 6, вариант 1
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — с. 109
Источник: Готман Э. Г., Скопец З. А. Решение геометрических задач аналитическим методом: Пособие для учащихся 9—10 кл. — М.: Просвещение, 1979. — № 62, с. 14
Источник: Прасолов В. В. Задачи по планиметрии. — 6-е изд. — М.: МЦНМО, 2007. — № 2.61(а), с. 37
Источник: Всесибирская физико-математическая олимпиада. — 2009, заключительный этап, задача 6, 11 класс
