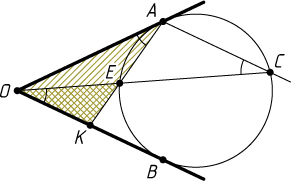
121. Дан угол с вершиной O
и окружность, касающаяся его сторон в точках A
и B
. Из точки A
параллельно OB
проведён луч, пересекающий окружность в точке C
. OC
пересекает окружность в точке E
. Прямые AE
и OB
пересекаются в точке K
. Докажите, что OK=KB
.
Указание. Треугольник KOA
подобен треугольнику KEO
.
Решение. Треугольники KOA
и KEO
подобны по двум углам (\angle EOK=\angle ACE=\angle OAK)
. Поэтому \frac{KE}{OK}=\frac{OK}{AK}
. Отсюда следует, что OK^{2}=EK\cdot AK
. С другой стороны, по теореме о касательной и секущей EK\cdot AK=KB^{2}
. Следовательно, OK=KB
.
Источник: Всесоюзная олимпиада по математике. — 1973, VII, 10 класс
Источник: Васильев Н. Б., Егоров А. А. Задачи всесоюзных математических олимпиад. — М.: Наука, 1988. — № 177, с. 51
Источник: Журнал «Crux Mathematicorum». — 1980, № 2, задача 9-2, с. 41
Источник: Всесибирская физико-математическая олимпиада. — 2012, заключительный этап, задача 4, 10 класс