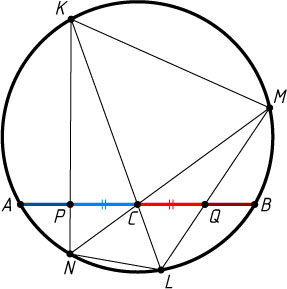
122. Задача о бабочке. Через середину C
произвольной хорды AB
окружности проведены две хорды KL
и MN
(точки K
и M
лежат по одну сторону от AB
). Отрезок KN
пересекает AB
в точке P
. Отрезок LM
пересекает AB
в точке Q
. Докажите, что PC=QC
.
Указание. Опустите перпендикуляры из точек P
и Q
на CK
, CN
и CM
, CL
соответственно и рассмотрите образовавшиеся пары подобных треугольников.
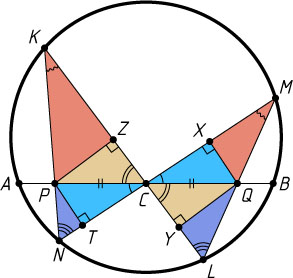
Решение. Первый способ. Пусть QX
и QY
— высоты треугольников CQM
и CQL
, а PZ
и PT
— высоты треугольников CPK
и CPN
(рис. 1). Треугольники CQX
и CPT
подобны по двум углам. Также по двум углам подобны треугольники CQY
и CPZ
с тем же коэффициентом подобия \frac{CQ}{CP}
. Поэтому
\frac{CQ}{CP}=\frac{QX}{PT}=\frac{QY}{PZ}.
Значит,
\frac{CQ^{2}}{CP^{2}}=\frac{QX}{PT}\cdot\frac{QY}{PZ}=\frac{QX}{PZ}\cdot\frac{QY}{PT}.
Из равенства углов NKL
и NML
, а также MLK
и MNK
следует, что треугольник MXQ
подобен треугольнику KZP
, а треугольник LYQ
подобен треугольнику NTP
. Поэтому
\frac{QX}{PZ}\cdot\frac{QY}{PT}=\frac{MQ}{KP}\cdot\frac{LQ}{NP}.
По теореме о равенстве произведений отрезков пересекающихся хорд
MQ\cdot LQ=AQ\cdot QB=(AC+CQ)(BC-CQ)=
=(AC+CQ)(AC-CQ)=AC^{2}-CQ^{2},
KP\cdot NP=BP\cdot AP=(BC+CP)(AC-CP)=
=(AC+CP)\cdot(AC-CP)=AC^{2}-CP^{2}.
Следовательно,
\frac{CQ^{2}}{CP^{2}}=\frac{AC^{2}-CQ^{2}}{AC^{2}-CP^{2}}.
После перемножения и приведения подобных получим, что CQ^{2}=CP^{2}
.
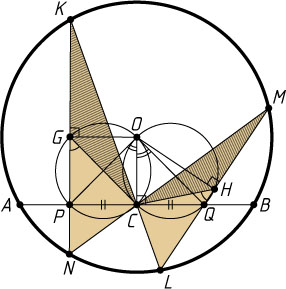
Второй способ. Опустим из центра O
данной окружности перпендикуляры OG
и OH
на хорды KN
и ML
соответственно (рис. 2). Тогда G
и H
— середины отрезков KN
и ML
. Рассмотрим случай, изображённый на рис. 2.
Проведём две окружности: через точки O
, C
, P
, G
и через точки O
, C
, Q
, H
. По теореме о вписанных углах \angle COP=\angle CGP
и \angle COQ=\angle CHQ
. Поскольку треугольники KCN
и MCL
подобны, то подобны и треугольники KCG
и MCH
, так как CG
и CH
— соответствующие медианы треугольников KCN
и MCL
. Поэтому
\angle CGP=\angle CHQ,~\angle COP=\angle COQ.
Значит, высота CO
треугольника POQ
является его биссектрисой. Поэтому треугольник POQ
— равнобедренный. Следовательно, PC=CQ
. Аналогично для всех других возможных случаев расположения точек K
, L
, M
и N
.
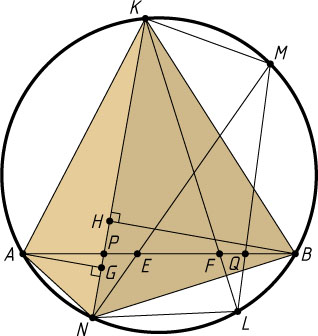
Третий способ. Докажем сначала следующее утверждение. Пусть хорда AB
пересекает противоположные стороны KN
, LM
и диагонали MN
и KL
вписанного четырёхугольника KMLN
в точках P
, Q
, E
и F
соответственно (рис. 3). Положим \frac{AP}{PB}=\alpha
, \frac{AQ}{QB}=\beta
, \frac{AE}{EB}=x
, \frac{AF}{FB}=y
. Тогда \alpha\beta=xy
.
Действительно, пусть AG
и BH
— высоты треугольников AKN
и BKN
, опущенные на общее основание KN
. Тогда \frac{AG}{BH}=\frac{AP}{BP}
, поэтому \frac{S_{\triangle AKN}}{S_{\triangle BKN}}=\frac{AP}{BP}
. С другой стороны,
\frac{S_{\triangle AKN}}{S_{\triangle BKN}}=\frac{\frac{1}{2}AK\cdot AN\sin\angle KAN}{\frac{1}{2}BK\cdot BN\sin\angle KBN}=\frac{AK\cdot AN}{BK\cdot BN}.
Следовательно, \alpha=\frac{AP}{PB}=\frac{AK\cdot AN}{BK\cdot BN}
.
Аналогично докажем, что
\beta=\frac{AQ}{QB}=\frac{AM\cdot AL}{BM\cdot BL},~x=\frac{AE}{EB}=\frac{AL\cdot AN}{BL\cdot BN},~y=\frac{AF}{FB}=\frac{AK\cdot AM}{BK\cdot BM},
значит,
\alpha\beta=\frac{AK\cdot AN}{BK\cdot BN}\cdot\frac{AM\cdot AL}{BM\cdot BL}=\frac{AK\cdot AN\cdot AM\cdot AL}{BK\cdot BN\cdot BM\cdot BL},
xy=\frac{AL\cdot AN}{BL\cdot BN}\cdot\frac{AK\cdot AM}{BK\cdot BM}=\frac{AK\cdot AN\cdot AM\cdot AL}{BK\cdot BN\cdot BM\cdot BL}.
Следовательно, \alpha\beta=xy
. Утверждение доказано.
Вернёмся к нашей задаче (рис. 4). Диагонали KL
и MN
в этом случае пересекаются в середине C
хорды AB
, т. е. точки E
и F
совпадают с точкой C
. Это значит, что x=\frac{AE}{EB}=1
и y=\frac{AF}{FB}=1
. Тогда по доказанному \alpha\beta=1
, т. е.
\frac{AP}{PB}\cdot\frac{AQ}{QB}=1,~\frac{AP}{AB-AP}\cdot\frac{AB-QB}{QB}=1,~\frac{AP}{AB-AP}=\frac{QB}{AB-QB},
откуда AP=QB
. Следовательно,
PC=AC-AP=BC-QB=CQ.
Что и требовалось доказать.
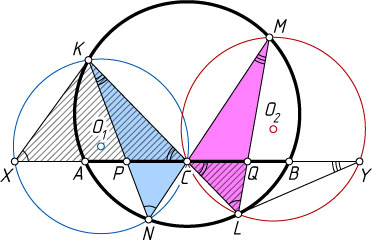
Четвёртый способ. (Решение Ф. Покровского.) Опишем окружности около треугольников CKN
и CML
(рис. 5). Пусть прямая AB
вторично пересекает первую из этих окружностей (с центром O_{1}
) в точке X
, а вторую (с центром O_{2}
) — в точке Y
.
Треугольник CLQ
подобен треугольнику CXK
по двум углам, так как \angle LCQ=\angle XCK
и
\angle CXK=\angle CNK=\angle MNK=\angle MLK=\angle QLK.
Значит, \frac{CQ}{CK}=\frac{CL}{CX}
, поэтому CQ\cdot CX=CL\cdot CK
. Аналогично треугольник LCY
подобен треугольнику PCK
, поэтому CL\cdot CK=CP\cdot CY
. Значит, CQ\cdot CX=CP\cdot CY
. Следовательно, равенство CP=CQ
равносильно равенству CX=CY
, и задача сводится к доказательству этого равенства.
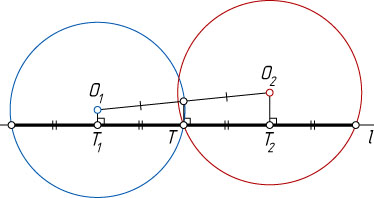
Лемма 1. Если прямая l
, проходящая через точку T
пересечения окружностей с центрами O_{1}
и O_{2}
, высекает на этих окружностях равные хорды, то отрезок, соединяющий точку T
с серединой O_{1}O_{2}
, перпендикулярен прямой l
.
Доказательство. Действительно, если T_{1}
и T_{2}
— проекции центров O_{1}
и O_{2}
на прямую l
(рис. 6), то T_{1}
и T_{2}
— середины равных хорд этих окружностей. Значит, T
— середина отрезка T_{1}T_{2}
, поэтому отрезок, соединяющий точку T
с серединой O_{1}O_{2}
, параллелен O_{1}T_{1}
и O_{2}T_{2}
. Следовательно, этот отрезок перпендикулярен прямой l
. Лемма доказана.
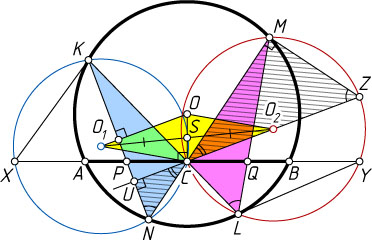
Лемма 2. Пусть O
— центр данной окружности. Тогда четырёхугольник OO_{1}CO_{2}
— параллелограмм.
Доказательство. Линия центров пересекающихся окружностей перпендикулярна их общей хорде, поэтому OO_{1}\perp KN
(рис. 7).
Пусть CZ
— диаметр окружности с центром O_{2}
, а прямая CZ
пересекает KN
в точке U
. Тогда
\angle CMZ=90^{\circ},~\angle NCU=\angle MCZ,
\angle CNU=\angle CNK=\angle MNK=\angle MLK=\angle MLC=\angle MZC.
Значит, два угла прямоугольного треугольника CMZ
соответственно равны двум углам треугольника CUN
, поэтому третий угол треугольника CUN
также прямой, т. е. \angle CUN=90^{\circ}
. Следовательно, CO_{2}\perp KN
. Таким образом, прямые OO_{1}
и O_{2}C
перпендикулярны одной и той же прямой, значит, OO_{1}\parallel O_{2}C
.
Аналогично OO_{2}\parallel O_{1}C
, следовательно, OO_{1}CO_{2}
— параллелограмм. Лемма доказана.
Пусть S
— точка пересечения диагоналей параллелограмма OO_{1}CO_{2}
. Тогда S
— середина O_{1}O_{2}
. Из леммы 1 и единственности перпендикуляра следует, что C
— середина отрезка XY
. Значит, CX=CY
. Что и требовалось доказать.
Источник: Шклярский Д. О., Ченцов Н. Н., Яглом И. М. Избранные задачи и теоремы элементарной математики. — Ч. 2: Геометрия (планиметрия). — М.: ГТТИ, 1952. — № 104, с. 33
Источник: Прасолов В. В. Задачи по планиметрии. — 6-е изд. — М.: МЦНМО, 2007. — № 2.66, с. 37
Источник: Коксетер Г. С. М., Грейтцер С. Л. Новые встречи с геометрией. — М.: Наука, 1978. — с. 59
Источник: Шарыгин И. Ф. Геометрия: 9—11 кл.: От учебной задачи к творческой: Учебное пособие. — М.: Дрофа, 1996. — № 483, с. 58
Источник: Журнал «Crux Mathematicorum». — 1981, № 10, с. 292-294






