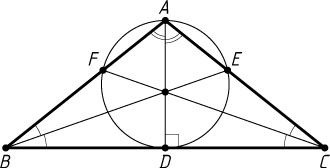
123. В равнобедренном треугольнике ABC
(AB=AC
) проведены биссектрисы AD
, BE
, CF
. Найдите BC
, если известно, что AC=1
, а вершина A
лежит на окружности, проходящей через точки D
, E
и F
.
Ответ. \frac{\sqrt{17}-1}{2}
.
Указание. Примените свойство биссектрисы треугольника и теорему о касательной и секущей.
Решение. Пусть BC=x
. По свойству биссектрисы треугольника \frac{CE}{AE}=\frac{x}{1}
. Отсюда находим, что CE=\frac{x}{1+x}
.
Поскольку CD^{2}=CE\cdot AC
, то
\left(\frac{x}{2}\right)^{2}=\frac{x}{1+x}.
Из этого уравнения находим, что
x=\frac{\sqrt{17}-1}{2}.
Источник: Вступительный экзамен на механико-математический факультет МГУ. — 1969, № 4, вариант 3
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — № 12.25, с. 95
