124. Дана окружность с диаметром AB
. Вторая окружность с центром в точке A
пересекает первую в точках C
и D
, а диаметр AB
— в точке E
. На дуге CE
, не содержащей точки D
, взята точка M
, отличная от точек C
и E
. Луч BM
пересекает первую окружность в точке N
. Известно, что CN=a
, DN=b
. Найдите MN
.
Ответ. \sqrt{ab}
.
Указание. Треугольники CNM
и MND
подобны.
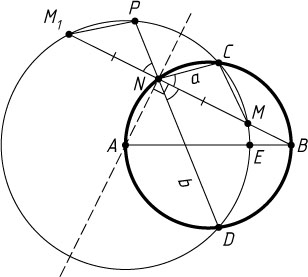
Решение. Пусть M_{1}
— ещё одна точка пересечения луча BM
со второй окружностью, а P
— точка пересечения этой окружности с лучом DN
.
Поскольку AN\perp MM_{1}
, то M_{1}N=MN
(диаметр, перпендикулярный хорде, делит её пополам), а так как B
— середина дуги CD
, не содержащей точки A
, то
\angle PNM_{1}=\angle BND=\angle BNC=\angle CNM.
При симметрии относительно прямой AN
точка M
переходит в M_{1}
, луч NC
— в луч NP
, а вторая окружность — в себя. Поэтому треугольник NCM
переходит в треугольник NPM_{1}
. Значит, эти треугольники равны. Поэтому PN=CN=a
.
По теореме о равенстве произведений отрезков пересекающихся хорд окружности
MN^{2}=MN\cdot NM_{1}=PN\cdot DN=CN\cdot DN=ab.
Следовательно, MN=\sqrt{ab}
.
Источник: Вступительный экзамен на физический факультет МГУ. — 1978, № 6, вариант 1
Источник: Шарыгин И. Ф. Геометрия: 9—11 кл.: От учебной задачи к творческой: Учебное пособие. — М.: Дрофа, 1996. — № 231, с. 27
Источник: Нестеренко Ю. В., Олехник С. Н., Потапов М. К. Задачи вступительных экзаменов по математике. — М.: Наука, 1986. — с. 29
Источник: Прасолов В. В. Задачи по планиметрии. — 6-е изд. — М.: МЦНМО, 2007. — № 2.65, с. 37
