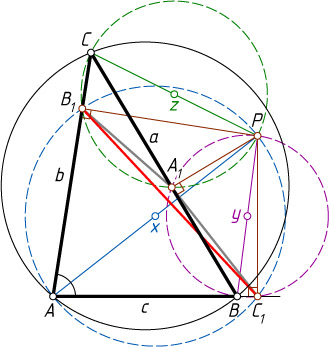
129. Из произвольной точки P
, не лежащей на описанной окружности, опущены перпендикуляры PA_{1}
, PB_{1}
, PC_{1}
на стороны треугольника ABC
или на их продолжения. Известно, что AB=c
, BC=a
, AC=b
, PA=x
, PB=y
, PC=z
. Найдите стороны треугольника A_{1}B_{1}C_{1}
, если радиус окружности, описанной около треугольника ABC
, равен R
.
Ответ. \frac{cx}{2R}
, \frac{ay}{2R}
, \frac{bz}{2R}
.
Указание. Точки A
, B_{1}
, P
и C_{1}
лежат на окружности с диаметром AP
.
Решение. Точки A
, B_{1}
, P
и C_{1}
лежат на окружности с диаметром AP=x
. Поэтому
C_{1}B_{1}=AP\sin\angle A=x\sin\angle A=\frac{xa}{2R}.
Аналогично найдём A_{1}C_{1}
и A_{1}B_{1}
.