131. Четырёхугольник ABCD
вписан в окружность радиуса R
. Его диагонали взаимно перпендикулярны и пересекаются в точке P
. Найдите AP^{2}+BP^{2}+CP^{2}+DP^{2}
и AB^{2}+BC^{2}+CD^{2}+AD^{2}
.
Ответ. 4R^{2}
; 8R^{2}
.
Указание. Обозначьте \angle ADB=\alpha
и выразите стороны четырёхугольника по формуле a=2R\sin\alpha
(или проведите диаметр DD_{1}
).
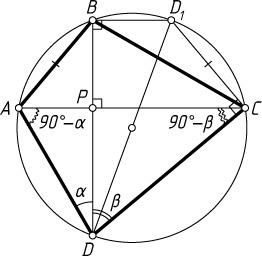
Решение. Первый способ. Обозначим \angle ADB=\alpha
, \angle BDC=\beta
. Тогда
AB=2R\sin\alpha,~BC=2R\sin\beta,~CD=2R\sin(90^{\circ}-\alpha)=2R\cos\alpha,
AD=2R\sin(90^{\circ}-\beta)=2R\cos\beta.
Следовательно,
AP^{2}+BP^{2}+CP^{2}+DP^{2}=AB^{2}+DC^{2}=
=4R^{2}\sin^{2}\alpha+4R^{2}\cos^{2}\alpha=4R^{2},
AB^{2}+BC^{2}+CD^{2}+AD^{2}=4R^{2}+4R^{2}=8R^{2}.
Второй способ. Проведём диаметр DD_{1}
. Поскольку BD\perp BD_{1}
и BD\perp AC
, то BD_{1}\parallel AC
, поэтому CD_{1}=AB
. Из прямоугольного треугольника DCD_{1}
находим, что
CD^{2}_{1}+CD^{2}=DD^{2}_{1}=4R^{2}.
Поэтому
AB^{2}+CD^{2}=4R^{2}.
Аналогично BC^{2}+AD^{2}=4R^{2}
. Следовательно,
AB^{2}+BC^{2}+CD^{2}+AD^{2}=4R^{2}+4R^{2}=8R^{2},
AP^{2}+BP^{2}+CP^{2}+DP^{2}=AB^{2}+DC^{2}=4R^{2}.
Третий способ. Пусть O
— центр окружности. Поскольку
\angle AOB+\angle COD=\smile AB+\smile CD=2\angle APB=2\cdot90^{\circ}=180^{\circ},
то, обозначив \angle AOB=\phi
, получаем, что \angle COD=180^{\circ}-\phi
. По теореме косинусов из треугольников AOB
и COD
получаем, что
AB^{2}=AO^{2}+OB^{2}-2AO\cdot OB\cos\phi=2R^{2}(1-\cos\phi),
CD^{2}=CO^{2}+OD^{2}-2CO\cdot OD\cos(180^\circ-\phi)=2R^{2}(1+\cos\phi).
Поэтому AB^{2}+CD^{2}=4R^{2}
. Аналогично BC^{2}+AD^{2}=4R^{2}
. Следовательно,
AB^{2}+BC^{2}+CD^{2}+AD^{2}=4R^{2}+4R^{2}=8R^{2},
AP^{2}+BP^{2}+CP^{2}+DP^{2}=AB^{2}+DC^{2}=4R^{2}.
