133. Четырёхугольник ABCD
, диагонали которого взаимно перпендикулярны, вписан в окружность с центром O
. Найдите расстояние от точки O
до стороны AB
, если известно, что CD=8
.
Ответ. 4.
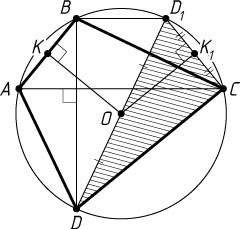
Указание. Проведите диаметр DD_{1}
.
Решение. Проведём диаметр DD_{1}
. Пусть K
и K_{1}
— проекции точки O
на хорды AB
и CD_{1}
соответственно. Поскольку BD_{1}
и AC
перпендикулярны DB
, то BD_{1}
параллельно AC
. Поэтому D_{1}C=AB
и OK_{1}=OK
.
Поскольку OK_{1}
— средняя линия прямоугольного треугольника DD_{1}C
, то
OK=OK_{1}=\frac{1}{2}DC=4.
Автор: Келарев А. В.
Источник: Московская математическая олимпиада. — 1979, XLII, 8 класс
Источник: Гальперин Г. А., Толпыго А. К. Московские математические олимпиады. — М.: Просвещение, 1988. — № 7, с. 140
Источник: Журнал «Квант». — 1979, № 9, с. 22, М582
Источник: Задачник «Кванта». — М582
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — № 3.23, с. 25
Источник: Прасолов В. В. Задачи по планиметрии. — 6-е изд. — М.: МЦНМО, 2007. — № 2.78, с. 38
