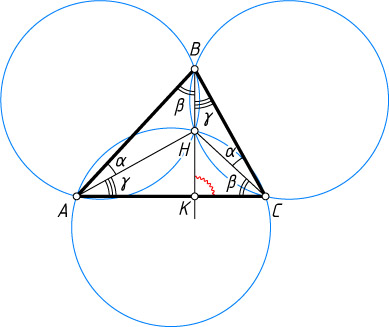
134. Три равные окружности имеют общую точку H
, а точки их пересечения, отличные от H
, образуют треугольник ABC
. Докажите, что H
— точка пересечения высот треугольника ABC
.
Указание. \angle BAH=\angle BCH,
\angle ABH=\angle ACH,
\angle CBH=\angle CAH.
Решение. Пусть ABC
— остроугольный треугольник. Заметим, что
\angle BAH=\angle BCH,~\angle ABH=\angle ACH,~\angle CBH=\angle CAH.
Обозначим эти углы \alpha
, \beta
, \gamma
соответственно. Тогда 2\alpha+2\beta+2\gamma=180^{\circ}
. Поэтому \alpha+\beta+\gamma=90^{\circ}
.
Пусть K
— точка пересечения прямой BH
с отрезком AC
. Тогда
\angle BKC=180^{\circ}-\alpha-\beta-\gamma=90^{\circ}.
Аналогично для неостроугольного треугольника.
Источник: Прасолов В. В. Задачи по планиметрии. — 6-е изд. — М.: МЦНМО, 2007. — № 3.25, с. 59
Источник: Прасолов В. В. Задачи по планиметрии. — Ч. 1. — М.: Наука, 1991. — № 3.24, с. 61
Источник: Шарыгин И. Ф. Геометрия: 9—11 кл.: От учебной задачи к творческой: Учебное пособие. — М.: Дрофа, 1996. — № 408, с. 49
