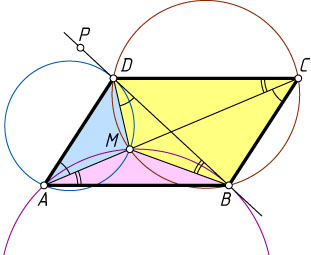
136. В параллелограмме ABCD
диагональ AC
больше диагонали BD
. Точка M
на диагонали AC
такова, что около четырёхугольника BCDM
можно описать окружность. Докажите, что BD
— общая касательная окружностей, описанных около треугольников ABM
и ADM
.
Указание. \angle MBD=\angle BAM
.
Решение. Поскольку
\angle MBD=\angle MCD=\angle BAM,
а точки A
и D
лежат по разные стороны от прямой BM
, то BD
— касательная к окружности, описанной около треугольника ABM
. Действительно, если бы это было не так, то взяв на касательной, проведённой в точке B
к этой окружности, точку P
, лежащую в той же полуплоскости относительно прямой BM
, что и точка D
, получили бы, что
\angle MBP=\angle BAM=\angle MBD,
что невозможно, так как от данного луча в заданную плоскость можно отложить ровно один угол, равный данному.
Таким образом, BD
— касательная к окружности, описанной около треугольника ABM
.
Аналогично докажем, что BD
— касательная к окружности, описанной около треугольника ADM
.
Источник: Прасолов В. В. Задачи по планиметрии. — 6-е изд. — М.: МЦНМО, 2007. — № 3.13, с. 57
