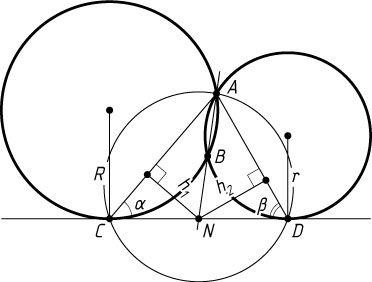
138. Две окружности радиусов R
и r
пересекаются в точках A
и B
и касаются прямой в точках C
и D
; N
— точка пересечения прямых AB
и CD
(B
между A
и N
). Найдите:
1) радиус окружности, описанной около треугольника ACD
;
2) отношение высот треугольников NAC
и NAD
, опущенных из вершины N
.
Ответ. \sqrt{rR}
, \sqrt{\frac{r}{R}}
.
Указание. Обозначим \angle ACN=\alpha
, \angle ADN=\beta
. Тогда \frac{\sin\alpha}{\sin\beta}=\sqrt{\frac{r}{R}}
.
Решение. Обозначим \angle ACN=\alpha
, \angle ADN=\beta
. Тогда
AC=2R\sin\alpha,~AD=2r\sin\beta,~\frac{AC}{\sin\beta}=\frac{AD}{\sin\alpha}~\Rightarrow~\frac{2R\sin\alpha}{\sin\beta}=\frac{2r\sin\beta}{\sin\alpha}.
Отсюда находим, что \frac{\sin\alpha}{\sin\beta}=\sqrt{\frac{r}{R}}
.
Если R_{1}
— радиус окружности, описанной около треугольника ACD
, то
R_{1}=\frac{AC}{2\sin\beta}=\frac{2R\sin\alpha}{2\sin\beta}=R\cdot\frac{\sin\alpha}{\sin\beta}=\sqrt{rR}.
По теореме о касательной и секущей
CN^{2}=NA\cdot NB,~DN^{2}=NA\cdot NB.
Поэтому CN=DN
. Если h_{1}
и h_{2}
— высоты, о которых говорится в условии задачи, то
\frac{h_{1}}{h_{2}}=\frac{CN\cdot\sin\alpha}{DN\cdot\sin\beta}=\frac{\sin\alpha}{\sin\beta}=\sqrt{\frac{r}{R}}.
Источник: Вступительный экзамен на физический факультет МГУ. — 1989, вариант 1, № 6
Источник: Нестеренко Ю. В., Олехник С. Н., Потапов М. К. Задачи вступительных экзаменов по математике. — М.: Факториал, 1995. — с. 51
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — № 12.32, с. 96
