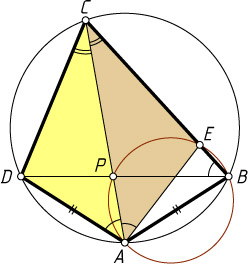
140. Во вписанном четырёхугольнике ABCD
через вершины A
, B
и точку P
пересечения диагоналей проведена окружность, пересекающая сторону BC
в точке E
. Докажите, что если AB=AD
, то CD=CE
.
Указание. \angle DCA=\angle BCA
, \angle DAC=\angle CAE
.
Решение. Поскольку AD=AB
, то \angle DCA=\angle BCA
. Кроме того,
\angle DAC=\angle DBC=\angle CAE.
Поэтому треугольники AEC
и ADC
равны по стороне (AC
— общая) и двум прилежащим к ней углам. Следовательно, CD=CE
.
Источник: Журнал «Квант». — 1991, № 1, с. 55, задача 2
