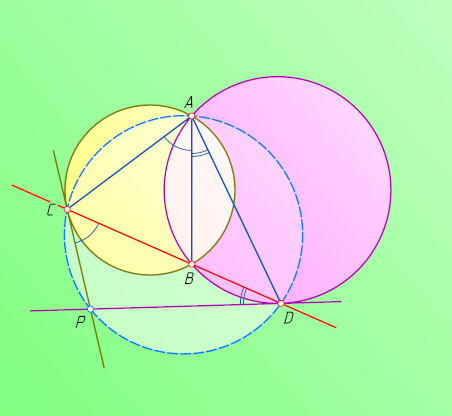
143. Две окружности пересекаются в точках A
и B
. Через точку B
проводится прямая, пересекающая вторично окружности в точках C
и D
, а затем через точки C
и D
проводятся касательные к этим окружностям. Докажите, что точки A
, C
, D
и точка P
пересечения касательных лежат на одной окружности.
Указание. Из теоремы об угле между касательной и хордой следует, что
\angle CAB=\angle DCP,~\angle BAD=\angle CDP.
Решение. Рассмотрим случай, когда точка B
лежит между C
и D
.
Из теоремы об угле между касательной и хордой следует, что
\angle CAB=\angle DCP,~\angle BAD=\angle CDP.
Поэтому
\angle CPD=180^{\circ}-(\angle DCP+\angle CDP)=180^{\circ}-\angle CAD.
Значит, четырёхугольник ACPD
— вписанный. Следовательно, точки A
, C
, D
и P
лежат на одной окружности.
Аналогично для остальных случаев.