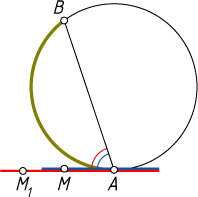
144. Точки A
и B
лежат на окружности, а точка M
— вне окружности. Известно, что угловая величина угла MAB
равна половине угловой величины дуги AB
, заключённой внутри этого угла. Докажите, что MA
— касательная к окружности.
Решение. Предположим, что это не так. Через точку A
проведём касательную к окружности и отметим на ней точку M_{1}
, лежащую по ту же сторону от прямой AB
, что и точка M
. По теореме об угле между касательной и хордой угол M_{1}AB
также равен половине угловой величины дуги заключённой внутри этого угла. Известно, что от данного луча в заданную полуплоскость можно отложить только один угол, равный данному, значит, лучи AM
и AM_{1}
совпадают. Следовательно, MA
— касательная к окружности. Что и требовалось доказать.